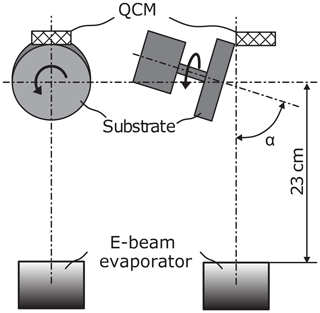
A schematic representation of the setup of the deposition system is presented in Fig. 1. The tantalum target is heated with an electron beam evaporator and transferred into the gas phase. The distance between the target and the substrate is 23 cm. The substrate is tilted at deposition angle α and is rotated rapidly at 10.5 rev min⁻¹. The deposition rate is monitored and kept constant during the entire deposition process using a quartz crystal monitor placed at a fixed position in the vacuum chamber.

We investigate two absorption layers – Ta80 and Ta85 – which have the following respective deposition angles: $\mathit{\alpha }={\mathrm{80}}^{\circ }$ and $\mathit{\alpha }={\mathrm{85}}^{\circ }$. Table 1 summarizes the conditions used for the deposition of these samples.

A substrate temperature above 30 % of the melting temperature of the target material increases the surface mobility of the impinging particles. In this case, the substrate temperature can be regarded as a further degree of freedom to influence the film structure (Hawkeye et al., 2014, p. 73). To reduce the degrees of freedom and for better reproducibility, the substrate is cooled actively so its temperature is held below 30 ^∘C during the evaporation. As a result, the diffusion length of the adsorbed particles on the substrate surface is reduced to a negligible level. The tantalum was deposed at a working pressure of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$– $\mathrm{7.5}\times {\mathrm{10}}^{-\mathrm{5}}$ Torr.

Table 1Conditions for the deposition of the Ta80 and Ta85 samples.

Download Print Version | Download XLSX

Figure 1Setup of the GLAD apparatus adapted from Schossig (2012a, p. 90) (QCM – quartz crystal monitor).

Download

FIB-SEM measurements are conducted using the Crossbeam NVision 40 field emission scanning electron microscope (FE-SEM) by Carl Zeiss with integrated advanced tomography package Atlas 5 3-D-Tomography. This equipment allows for high-resolution 3-D images with defined pixel sizes in all directions to be recorded.

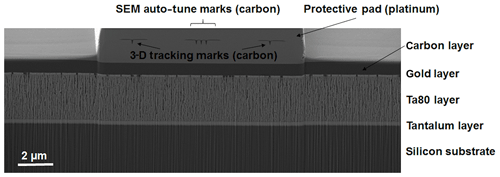
For minimization of charging effects and sample drift during the long measurement period, the sample is first fixed and electrically conducted by conductive silver. In addition, the whole sample surface is coated by an approximately 100 nm thick gold layer. For the protection of the 3-D preparation area and to ensure sharp-edge FIB cuts, an approximately $\mathrm{30}\mathrm{\mu }\mathrm{m}\times \mathrm{15}\mathrm{\mu }\mathrm{m}\times \mathrm{0.5}\mathrm{\mu }\mathrm{m}$ local carbon layer is applied by ion beam deposition.

Finally, a platinum layer with carbon marks is deposited for automated slice thickness control, auto-focus, and auto-stigmation functions using the SEM “AutoTune” and “3-D Tracking Marks” tools from the Zeiss Atlas 5 software (Carl Zeiss Microscopy, 2019). A cross-section of the final, prepared Ta80 sample is shown in Fig. 2.

Figure 2Setup for the automated SEM/FIB experiments exemplified by sample Ta80.

Download

For the Ta80 and Ta85 samples, respective data sets of 500 and 700 (3800 pixel × 1480 pixel) SEM slices are captured at a resolution of $\mathrm{10}\mathrm{nm}\times \mathrm{12.7}\mathrm{nm}\times \mathrm{10}\mathrm{nm}$. The FIB/SEM parameters are adapted manually and optimized for the tantalum as there are no standard conditions for FIB/SEM. In particular, parameters have to be optimized for the dissipation of the electric charge introduced by the electron beam and for reducing sample charging and sample drift so that the sample remains constant under the electron beam for hours. Thus, for the tantalum samples, the SEM is operated at a 2 keV acceleration voltage, and the FIB current is 1.5 nA with a slice thickness resolution of 10 nm. For all experiments, the secondary electron (SE) and the Inlens SE detectors are applied simultaneously. Both samples are imaged under the same conditions to ensure comparability. The images show not only the material to be analyzed but also the surroundings; thus, the segmentation is performed on a subset of the data sets referred to as the region of interest.

For the reconstruction of the porous 3-D structure, only the secondary electron (SE) images are used due to their superior gray value contrast compared with the Inlens SE detector images.

Throughout the paper, the following coordinate system is used: the x direction is parallel to the substrate, the y direction is parallel to the nano-rods' growth, and the z direction corresponds to the stacking direction.

Figure 3 shows representative slices of the samples. The Ta80 data set (Fig. 3a) is strongly compromised by curtaining artifacts in the same size range as the structure. Thus, decurtaining is indispensable in this sample. The Ta85 data set (Fig. 3b) also features curtaining artifacts. However, they have less impact due to the coarser structure and, therefore, do not need special attention.

Figure 3Representative xy slices from the SE image stacks for (a) Ta80 and (b) Ta85.

Download

In addition to being coarser, Ta85 is more porous. Therefore, shine-through artifacts are present in this sample. Algorithms to reconstruct the structure in spite of these artifacts are available (Prill et al., 2013; Salzer et al., 2015). Nevertheless, these algorithms require several parameters and can introduce artificial anisotropy as they were devised to detect features along the z direction.

Thus, we exploit the elongated pore shape in the Ta85 sample to introduce an alternative method that can extract the shine-through artifacts, allowing reconstruction by global thresholding.

4.2 Reconstruction of sample Ta80

For Ta80, a dedicated decurtaining algorithm is needed as state-of-the-art methods (Münch et al., 2009; Fitschen et al., 2017; Liu et al., 2018) fail due to the singular vertical shape of the structure and pores, which are in the same size range. Our method thrives on the layered structure of the sample, resulting in three regions of interest in the image: the top of the slices, which is free of curtaining; the central region holding the porous structure with curtaining artifacts; and the bottom region with curtaining artifacts and with similar gray values to the top region.

Figure 4Decurtaining of Ta80. A slice from the original Ta80 sample showing the objective and constraint regions (a). The slice after the decurtaining algorithm (b) and binarization (c).

Download

More precisely, from the bottom to top in the y direction, we have the silicon substrate, the solid tantalum layer, the porous tantalum forming the actual optical layer, the sputtered gold layer, and, finally, the carbon layer (see Fig. 2). As it is on the top, the carbon layer is not affected by curtaining (see Fig. 4a). The gray values of the carbon layer and the silicon substrate are nearly equal, as silicon and carbon are both nonmetallic elements with almost the same density. Thus, our decurtaining algorithm proceeds as follows:

1. A region of interest (ROI) is cropped, as shown in Fig. 4a. This ROI should contain the top and bottom regions with equal or similar intensity (carbon and silicon layers).

2. The top layer (without curtaining) is selected as a constraint region, and the bottom layer (with curtaining) is selected as an objective region.

3. The curtaining artifacts are then removed column-wise by the next two steps:

   • a.

     compute the gray value means m_c and m_o for the constraint and objective regions within the current column;

   • b.

     add m_c−m_o to all pixel gray values in the current column.

If the current column features a dark artifact, then m_c>m_o and the correction increases the gray values in the column. If the current column features a bright artifact, then m_c<m_o and the correction decreases the gray values in the column. The ROI selected in the first step of the algorithm is the same as that described above at the end of the Sect. 3. The results are shown in Fig. 4b.

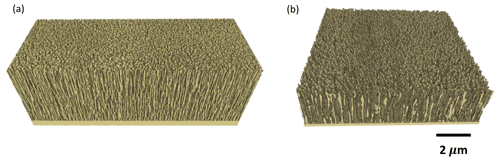
The decurtained sample Ta80 is directly reconstructed using global thresholding (Fig. 4c). We choose the threshold value manually such that the typical shape of the nano-rods (as narrow vertical structures with small embedded pores) is preserved. Figure 7a shows a volume rendering of the reconstruction.

4.3 Reconstruction of sample Ta85

Sample Ta85 is more porous and coarser than sample Ta80. Hence, global thresholding cannot be applied directly because of the shine-through artifacts. Here, we can exploit the particular elongated pore shape and structural width of the sample to remove the shine-through artifacts in a preprocessing step. This allows us to subsequently binarize by using global thresholding.

Figure 5a shows an xz slice of the Ta85 image. Here, we observe a vertical pattern of the structure, where the deep pores are identified by dark regions. Shine-through artifacts and solid phase are visible as well. However, the solid and the pore phases have nearly constant gray values, whereas shine-trough artifacts have gray values that increase vertically. Thus, we remove them by filtering as follows: we increase the visibility of edges, surface details, and reduce the noise in the images by applying a difference of Gaussians, which consists of the subtraction of two blurred images obtained by applying Gaussian blurring on the original images at specified σ₂ and σ₁.

This algorithm is typically applied with a size ratio of 4:1 for σ₂ to σ₁. Thus, the sigma sizes are ${\mathit{\sigma }}_{\mathrm{2}}=(\mathrm{4},\mathrm{1},\mathrm{4})$ and ${\mathit{\sigma }}_{\mathrm{1}}=(\mathrm{1},\mathrm{1},\mathrm{1})$, where the first component belongs to the x direction, the second belongs to the y direction, and the third belongs to the z direction. Figure 5b shows a representative slice after filtering using difference of Gaussians.

Subsequently, we apply a morphological fill-holes operation that removes all regional minima which are not connected to the image border (Soille, 1999). The regional minima are obtained by subtracting the input stack from the stack to which fill-holes has been applied (Fig. 5c). This image shows regions that definitely belong to the pore phase in black. Still, the nonzero regions contain shine-through artifacts.

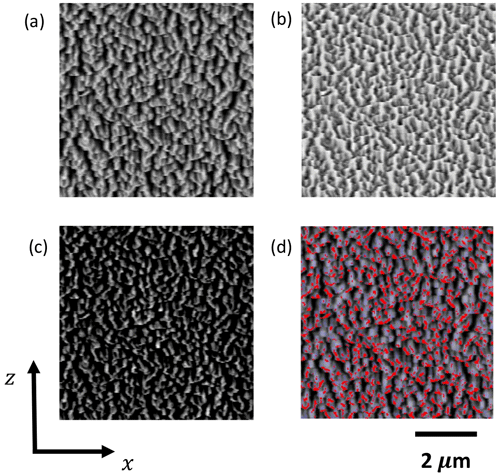
Figure 5Ta85 xz profiles: (a) the original stack, (b) after difference of Gaussians, (c) after the subtraction of fill-holes, and (d) the overlapped image (red represents the matrix phase, and blue represents the extracted shine-through artifacts).

Download

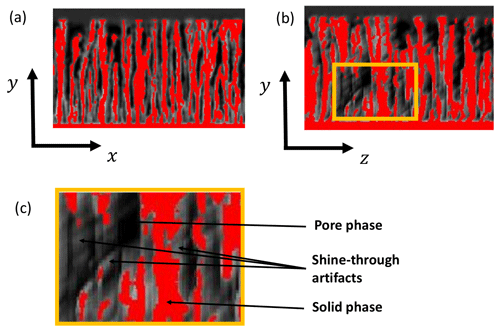
Figure 6Reconstruction result of the Ta85 sample shown as a red overlay on the gray value slices: (a) xy direction, (b) yz direction, and (c) a close-up of the yz direction.

Download

Figure 7Volume renderings of the reconstructed Ta80 and Ta85 samples. (a) Ta80: $\mathrm{10}\mathrm{\mu }\mathrm{m}\times \mathrm{4}\mathrm{\mu }\mathrm{m}\times \mathrm{4}\mathrm{\mu }\mathrm{m}$. (b) Ta85: $\mathrm{6}\mathrm{\mu }\mathrm{m}\times \mathrm{2}\mathrm{\mu }\mathrm{m}\times \mathrm{6}\mathrm{\mu }\mathrm{m}$.

Download

Figure 8Highly resolved SEM images and binarizations of the absorption layers. Pixel edge lengths 3 nm. (a) Sample Ta80. (b) Binarization of (a). (c) Sample Ta85. (d) Binarization of (c). The tantalum component of Ta80 appears thinner than that of sample Ta85. Moreover, pores in Ta85 grow bottom up.

Download

We extract them using a white top-hat transform, which removes small elements and details from images given a suitable structuring element. This morphological operation considers the difference of the original image and its morphological opening. The structuring element for the opening can be chosen according to the shape of the artifacts, which are extended in the z direction. A cuboid of size $(x,y,z)=(\mathrm{3},\mathrm{1},\mathrm{5})$ has given good results for the extraction of the artifacts. Figure 5d shows shine-through artifacts (blue) and the solid phase (red) overlapped.

After removing the shine-through artifacts, the images are segmented by global gray value thresholding with a manually chosen threshold. See Fig. 6 for the results. A volume rendering of the reconstructions is show in Fig. 7b.

4.4 Porosity validation

We use highly resolved 2-D images of the Ta80 and Ta85 samples with a 3 nm × 3 nm pixel size to validate our reconstructions regarding the porosity. The samples considered here belong to smaller thin films deposited with the same conditions as those presented above. For sample Ta80, the maximum height of the smaller version is 1400 nm. We denote this sample as Ta80a.

Figure 8a and c show these highly resolved 2-D images. They are segmented by applying a manually chosen global threshold as shown in Fig. 8b and d. Porosities regarding the height of these images are shown in Fig. 9a. Here, a height of 0 nm represents the height at which the substrate ends. Figure 9b shows the mean porosity in xz slices along the height y for the 3-D case.

For sample Ta80, the porosity of the highly resolved 2-D image varies (40 %±9 %), whereas the average porosities of the 3-D case are around 48 %, i.e., the porosities are consistent. For sample Ta85, the porosity in the 2-D case remains around 61 %±5 % for low to middle heights, while for high heights the porosity increases. In the 3-D case, the average porosity stays close to 65 % with a tendency to increase with the height following the previously described trend.

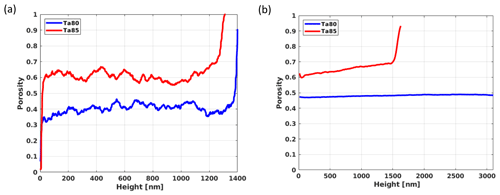
Figure 9Porosities as functions of the height over the substrate: (a) Porosity in 1-D segments of the 2-D images from Fig. 8b and d. (b) Porosity in xz slices of the reconstructed FIB-SEM stacks. Porosity remains nearly constant for Ta80, whereas it increases with height for Ta85.

Download

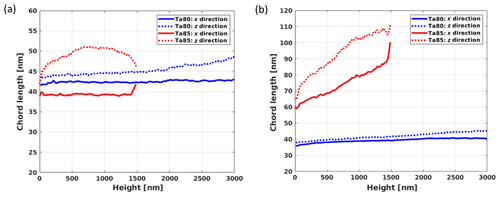
Figure 10Slice-wise mean chord lengths in the x and z directions as functions of the height above the substrate for the solid phase and pore phase of the reconstructed FIB-SEM stacks: (a) solid phase and (b) pore phase. For Ta80, mean chord lengths do not vary strongly. Only the solid phase tends to be more elongated in the z direction with increasing height. For Ta85, both the solid phase and the pore phase are elongated in the z direction. Moreover, pore sizes clearly grow with height.

Download

Porosity provides a first insight concerning structural differences between the samples. Indeed, Fig. 9b shows that sample Ta80 is less porous than sample Ta85 (by nearly 20 %) with a noticeable increase with height. Nevertheless, this measure is insufficient for sample characterization. To quantitatively measure both samples, we determine the mean thickness and the mean pore size at different heights above the substrate. For this reason, we compute the mean chord lengths for the solid and pore phases. The mean chord length is the expectation of the length of the typical chord obtained when intersecting the structure with lines in a given direction (see e.g., Ohser and Schladitz, 2009). Elongated structures have a larger mean chord length in the direction of their elongation.

In particular, we study the mean chord lengths in the x and z directions as functions of the heights as show Fig. 10a and b. For sample Ta80, the mean chord lengths tend to be stable in the sense that they remain in the 42±10 nm and 38±10 nm intervals for the solid phase and pore phase, respectively. Conversely, for sample Ta85, the mean chord lengths of the pore phase increase with height as shown in Fig. 10b.

Furthermore, in both samples, we observe an artificial anisotropy. More precisely, the mean chord lengths in the x  and z directions should be equal but differ by almost 7 % and 18 % for Ta80 and Ta85, respectively. For sample Ta80, this is due to imperfectly removed curtaining biasing the chord lengths in x direction downwards, whereas for sample Ta85, the underestimation in x direction is originates from curtaining.

For our structural comparison, this is not crucial as both samples are affected. However, this source of error has to be taken into account or corrected for, e.g., when simulating macroscopic material properties (Prill et al., 2019).

To obtain more information about the spatial arrangement of the nano-rods, we compute the spherical contact distribution for the pore phase, which is defined as follows: if we denote the 3-D structure as Ξ, and the unit ball centered in the origin as B∈ℝ³, the spherical contact distribution is given by

H_b(r) denotes the probability of reaching the solid phase from a randomly chosen point of the pore phase within a distance less than or equal to r (Ohser and Mücklich, 2000). It can be estimated efficiently using a linear time Euclidean distance transform algorithm.

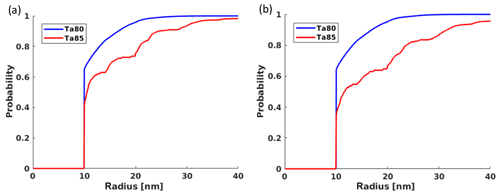
Figure 11Spherical contact distributions for the pore space in the xz slice at (a) 600 nm and (b) 1200 nm over the substrate. At these heights, Ta85 is clearly coarser than Ta80. Values less than 1 pixel are not considered – they are not reliable due to the fact that the data sets' resolution does not allow for structural details as small as pores to be differentiated.

Download

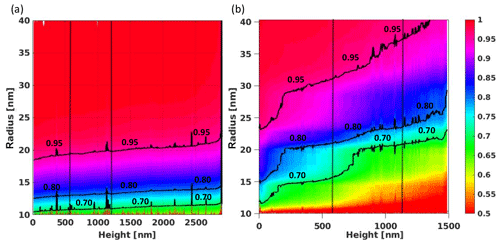
Figure 12Spherical contact distributions in xz slices as functions of the height over the substrate. Values of the spherical contact distributions given by the color map. The 70th, 80th, and 95th percentiles are delineated. Vertical lines at 600 and 1200 nm indicate the location of the curves represented in Fig. 11. Panel (a) represents Ta80, and panel (b) represents Ta85. For Ta80, the spherical contact distributions do not change significantly with height. The probability of reaching the solid within 20 nm of a random point in the pore space is nearly 1. For sample Ta85, this distance is considerably larger than in Ta80. Moreover, it clearly increases with height, which means that the comparably coarse pore structure becomes even coarser from bottom to top.

Download

In our data, the pore space is only a few pixels thin which leads to overly rough estimated distributions when using conventional distance transform algorithms. Using a sub-pixel precision leads to better resolved distributions (Lindblad and Sladoje, 2015; Godehardt et al., 2019). Figure 11 shows the spherical contact distribution at 600 and 1200 nm for both samples. Analyzing the spherical contact distributions for all heights yields Fig. 12, where the colors denote the values of H_b(r). This, the spherical contact distribution again emphasizes that sample Ta85 is coarser than Ta80 and coarsens with increasing height. Namely, a deposition angle of 80^∘ leads to structural similarity along the height, whereas a higher deposition angle of 85^∘ leads to pore structure coarsening.

Data are available upon request.

TO and SH designed and acquired the samples used in this study. DR, CR, KS, and MG performed the image processing, segmentation, and analysis of the reconstructed samples. TO, DR, KS, and SH wrote the paper with contributions from all authors. All authors contributed to the discussions.

The authors declare that they have no conflict of interest.

This research has been supported by the German Federal Ministry of Education and Research (grant no. 03VP00491/5), the German Academic Exchange Service (DAAD; Mathematics in Industry and Commerce Ph.D. program), and the German Research Foundation (grant no. GE 779/32).

This paper was edited by Ulrich Schmid and reviewed by two anonymous referees.