the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
SimOptDevice: a library for virtual optical experiments
Reyko Schachtschneider
Manuel Stavridis
Ines Fortmeier
Michael Schulz
Clemens Elster
Virtual experiments have become an indispensable tool for the design and the accuracy assessment of novel measurement procedures and instruments. Virtual experiments are particularly relevant in modern optics due to its challenging demands for highly accurate measurements. This paper introduces SimOptDevice, a flexible library for opto-mechanical virtual experiments. After describing the scope and general structure of the library, its underlying mathematical tools used for solving the related numerical tasks are described. Finally, the application of SimOptDevice to a recent interferometric measurement procedure is presented.
The author's copyright for this publication is transferred to the Physikalisch-Technische Bundesanstalt (PTB).
Following the advance of technology and the demand for highly accurate measurements, optical instruments and experiments have become very complex in recent years. In addition, sophisticated data analysis has become an important part of modern optical measurement devices. To ensure that a measurement principle is fit for its purpose, it is beneficial to first test it in a virtual environment prior to building the physical setup. That way, experimenters can save time and costs in the development of novel procedures. Furthermore, virtual experiments are often essential for the assessment of accuracies that can be reached.
For these reasons, virtual experiments have become an important tool in optics. Examples of applications are non-null interferometer calibration (Hao et al., 2016), validation of new data analysis techniques (Shen et al., 2015), absolute flatness measurements of optical surfaces (Bouillet and Morin, 2014), and accuracy evaluations in interferometric measurements (Wiegmann et al., 2011) or deflectometric flatness measurements (Schulz et al., 2010). Virtual experiments have become essential also in many other scientific fields, e.g. simulations of X-ray optics experiments (Knudsen et al., 2013), neutron scattering (Lieutenant et al., 2004), uncertainty assessment in computer tomography (Hiller and Reindl, 2012) or coordinate measurement machines (Heißelmann et al., 2017; Trenk et al., 2004), cross-borehole imaging (Donato and Crocco, 2015), or error quantification of CNC milling machines (Soori et al., 2013).
The Physikalisch-Technische Bundesanstalt (PTB) has developed the SimOptDevice software library for optical virtual experiments. SimOptDevice is a flexible library implemented in MATLAB® (MATLAB, 2018) that covers a large range of applications. It facilitates the design of experiments and allows one to develop and test measurement procedures. Furthermore, SimOptDevice is used to optimize existing measurement procedures with respect to measurement time and uncertainty. The latter is particularly relevant for PTB, which aims at measurements at the highest level of accuracy. Successful examples using SimOptDevice include accuracy evaluation of interferometric measurements of a synchrotron mirror (Wiegmann et al., 2011), development of a deflectometric flatness reference at PTB (Schulz et al., 2010; Ehret et al., 2012), and accuracy tests for multi-spectral imaging systems (Dierl et al., 2018).
In this paper we will describe the structure of SimOptDevice and its underlying mathematical methods. We will address the key issues of optical virtual experiments and refer to the corresponding solutions implemented in SimOptDevice. The purpose of this paper is to describe the mathematical methods necessary for implementing a complex optical simulation environment, enabling readers to set up a software solution of their own.
The general structure of SimOptDevice and its basic principles are described in Sect. 2. In Sect. 3 we introduce the mathematical methods used for the solution of related numerical problems. A prominent example is then presented in Sect. 4. Finally, some conclusions are given.
The SimOptDevice library can be used to perform virtual optical measurements with complex beam paths running through a series of optical elements. It considers nested scanning stages accounting for translations and rotations, and supports the use of various sensors such as cameras. SimOptDevice is based on the application of ray optics.
The basic principle of SimOptDevice is a system of hierarchical coordinate systems, combined with ray tracing routines. Within each coordinate system, optical elements can be placed. A related local coordinate system is assigned to each considered optical element, along with a superordinate coordinate system relative to which the local coordinate system is defined. In this way, a tree structure of coordinate systems is built. Each local coordinate system can undergo individual rotations and translations with respect to its superordinate system. The coordinates of each element can be transformed into any of the other employed coordinate systems. Those transformations are made simple by using homogeneous coordinates which are introduced in Sect. 3.1.
The power of SimOptDevice lies in tracing rays and performing ray aiming accurately and efficiently according to the laws of refraction and reflection while being in control of all optimization parameters and the applied algorithms. Using the library for our experiments, we view and verify all intermediate results, which is very helpful for tuning the algorithms for each specific problem. Whereas ray tracing follows a ray through the optical system when start point and direction are given, ray aiming seeks the path through the system for given start and end points. The latter is a highly nonlinear optimization problem. Details are described in Sect. 3.
The accurate modelling of all elements of a measurement setup is another advantage of SimOptDevice. This includes not only optical elements like lenses, mirrors and sensors but also linear stages and rotary tables. Ensembles of elements can be saved and reused in other virtual experiments.
During development, the software has been successfully checked against ray tracing results obtained by ZEMAX. This included comparisons of optical path lengths and of points reached by ray tracing. The differences were in the sub-nanometre range.
3.1 Coordinate transformations
One key feature of SimOptDevice is its easy way to transform coordinates from any local system to any other coordinate system within the defined structure (see Fig. 1). Coordinates are defined as homogeneous coordinates (see e.g. Cox et al., 2007, p. 357 ff.). Rotations and translations can be represented as matrices, and it is simple to connect transformations and compute a transformation's inverse. Homogeneous coordinates for describing points in ℝ3 have four components. A vector v=(x, y, z)T is represented in homogeneous coordinates as , , w)T, where w≠0 is arbitrary and , , and . Usually, w is set to one.
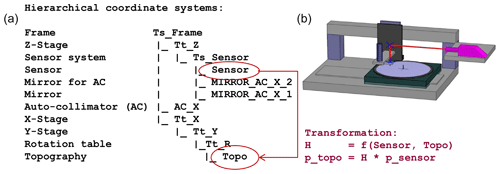
Figure 1Example of the hierarchical structure of coordinate systems in SimOptDevice. (a) The plot of a coordinate system tree example is shown. The left column lists the element names; the right column shows a sketch of the hierarchical structure of the coordinate systems. (b) The corresponding instrument is illustrated. The position and orientation of each of the instrument's subsystems are defined with respect to the superordinate system through a transformation of homogeneous coordinates. A transformation matrix H can be computed for transformations from one system to another (see Eq. 2). It is a function of the source system and the destination system (in this example Sensor and Topo, respectively). The common superordinate system Ts_Frame is needed for the computation of the transformation matrix (cf. Eq. 2). Subsequently, coordinates of a point in one system can be transformed to any other system by multiplication by the corresponding transformation matrix H.
With this coordinate definition, a translation or rotation is represented by a 4×4 matrix:
Rotations about the other axes are defined analogously. The composition of several homogeneous transformations H1, H2, …, HN is equal to a single homogeneous transformation
Using Eq. (1), the translation and rotation of a coordinate system with respect to its superordinate system are represented by a single matrix. The inverse of a homogeneous transformation is represented by the inverse of the corresponding transformation matrix. The aforementioned transformation from one local source system Sa to another destination system Sb is performed with the help of a common superordinate system Sc:
For a more comprehensive introduction to homogeneous coordinates, see e.g. Cox et al. (2007) or Hartley and Zisserman (2003).
3.2 Ray tracing
Ray propagation through the defined object is performed by sequential ray tracing. For this tracing method the order of elements passed by a ray is known in advance and optical paths are computed element by element. SimOptDevice computes the ray paths locally in each optical element system. At the boundary Ti between two elements (e.g. a surface of a lens), the current intersection point pi of the ray with that boundary along with the new ray direction ei are calculated in the new local system (cf. Sect. 3.1). The ray is then traced until it intersects with the next boundary, and so on. The intersection point with Ti and the new direction are a function of the previous intersection point and ray direction:
Function fi entails performing the following steps (cf. Fig. 2 for an illustration):
-
transformation of pi−1 and ei−1 from system Ti−1 to Ti,
-
calculation of the ray's geometrical path length li between Ti−1 and Ti,
-
determination of next intersection point ,
-
calculation of normal vector ni on Ti in pi, and
-
calculation of the new ray direction ei according to the laws of refraction and reflection.
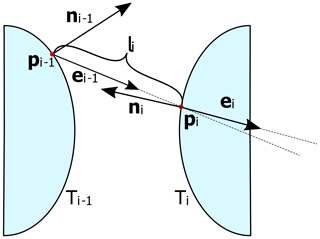
Figure 2Schematics of a ray tracing step. Each topography T has its own coordinate system. The intersection point pi with topography Ti is computed from the previous intersection point pi−1 and the previous ray direction ei−1. Subsequently, the new ray direction ei at Ti is computed according to the laws of reflection and refraction.
This is classical ray tracing with the particular feature that at each boundary the intersection point and the new direction are calculated in the new local coordinate system. Step 3 is calculated analytically for planes and spherical surfaces and has to be calculated numerically for more complex surfaces like Zernike surfaces, aspheres, or surfaces described by a Gauss function. If the ray passes N surfaces, there are N different functions fi. The last intersection point and ray direction can be expressed as a function of the start point and direction by concatenation of functions f1 to fN:
Furthermore, for each crossing of a boundary Ti a Jacobian matrix containing the partial derivatives of the intersection point pi and the ray direction ei with respect to the previous intersection point pi−1 and the previous ray direction ei−1 is calculated. It is associated with Eq. (3) and has the following form:
where xi and yi are the x and y components of the point pi, and and are the x and y components of the direction ei. We only need the derivatives with respect to the x and y components, since the intersected topographies are known and the z component is fixed at the intersection point. Since the direction vector has unit length, its z component can be calculated by . The Jacobian matrix J corresponding to the concatenation of N−1 interfaces i=1 … N−1 associated with Eq. (4) is obtained by multiplication of the corresponding matrices:
The inverse Jacobian matrix J−1 describes partial derivatives of the ray's behaviour along the same path in the opposite direction. These Jacobian matrices are used extensively when performing the ray aiming. Their usage is explained in more detail in Sect. 3.3. A detailed description of the ray tracing and ray aiming procedures can also be found in Fortmeier (2016, in German).
3.3 Ray aiming
Given a start point p0 and an end point the task of ray aiming is to find the start direction e0 from p0 in order to minimize the distance between pN and the desired end point (see Fig. 3):
where denotes the Euclidean norm and pN is reached through application of ray tracing for a chosen start direction e0. For successful ray aiming the resulting norm in Eq. (6) is close to zero. This is usually a highly nonlinear problem. It can be solved using one of MATLAB®'s parallel nonlinear solver routines, e.g. lsqnonlin. The latter is a solver for nonlinear least-squares problems in which the trust-region-reflective or Levenberg–Marquard algorithm can be applied. For better convergence of the solver, the ray tracing Jacobian matrix from Eq. (5) is utilized in this step. The Jacobian matrices calculated during ray tracing are used to update the start direction e0 when minimizing the distance between point pN and point . Furthermore, SimOptDevice delivers the Jacobian matrices for the change in total optical path lengths with respect to changes in a point pi or a ray direction ei for each surface Ti (Fortmeier et al., 2014). It is calculated analytically, thereby omitting the computationally expensive extra ray tracing steps for the numerical differentiation. The Jacobian matrices for ray aiming are important in many interferometric applications, e.g. the tilted-wave interferometer (cf. Sect. 4), where the change in the optical path length of a ray is a significant quantity of the experiment.
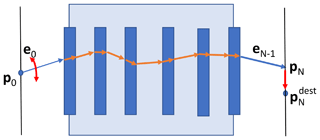
Figure 3Ray aiming principle: the start and end points p0 and of a ray are given. The task is to find the correct start angle e0 such that the desired end point is hit. This is achieved by minimizing the distance between points pN and , when pN is reached through application of ray tracing for a chosen start direction, e0.
A requirement for successful ray aiming is that the destination point can be reached. Therefore, the valid area on the CCD (or any other final surface) is determined in a preceding step. A ray aiming between the light source and some characteristic points at the smallest aperture in the optical system is performed. The final ray directions at the aperture are used to trace the rays to the CCD, thereby defining the area that can be reached by rays from the sources. A ray aiming is regarded as successful if the norm of the difference in Eq. (6) is smaller than 1 nm. Local minima that prevent the algorithm from converging are detected and such rays are masked. Using the Jacobian matrix, the ray aiming usually converges in about four steps. Without the Jacobian matrix this takes approximately 12 to 15 steps, depending on the particular situation.
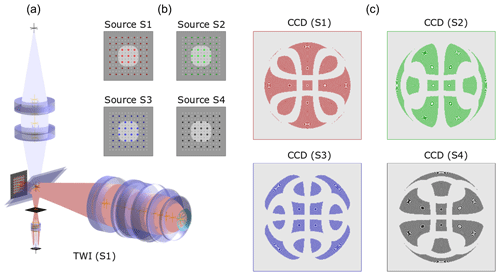
Figure 4Examples from the tilted-wave interferometer (TWI) simulation. (a) Ray paths through the instrument. Source array, reference and test arms, and detector (CCD). (b) The sources of the laser array are switched on in four groups (S1 to S4); (c) simulated interferograms on the CCD for each of the source groups for an asphere example.
The tilted-wave interferometer (TWI) is an interferometric measurement device for form measurements of asphere (Garbusi et al., 2008) and freeform surfaces. Figure 4 illustrates the simulation of interferograms for a measurement of an asphere. For SimOptDevice, the TWI is a particular application example since virtual experiments are not only used for designing the instrument and measurement setup, but are also an integrated part of data analysis. More precisely, we use SimOptDevice to obtain a numerical model of the experiment in dependence on the unknown form of the asphere or freeform surface under test. The latter is retrieved as the solution of a nonlinear inverse problem where in our implementation SimOptDevice constitutes the model. The inverse problem is solved iteratively, which is facilitated through the parallel computing capabilities of SimOptDevice. The nonlinear problem is linearized with the help of Jacobian matrices (Fortmeier et al., 2014). The solution of the inverse problem is found with the MATLAB® routine fsolve. It is possible to use different solver algorithms with fsolve. We typically choose trust-region-dogleg or trust-region-reflective. Trust region algorithms locally approximate the cost function by a quadratic function and progress towards the minimum of this approximation.
In order to accomplish an accurate recovery of the specimen surface, it is necessary to obtain an accurate model of the TWI (Garbusi et al., 2008). Differences between the numerical model of the instrument and the actual instrument have to be characterized very accurately prior to a measurement. For this calibration process, well-known test specimens (typically spheres) are measured with the TWI (Baer et al., 2014). The numerical model is then updated by adjusting the Zernike polynomial parametrization of two reference surfaces in order to account for the remaining discrepancies.
SimOptDevice has also been used for uncertainty evaluation (Fortmeier et al., 2017) of the TWI and for the exploration of new measurement concepts with the TWI (Fortmeier et al., 2016).
SimOptDevice is a versatile library for conducting virtual opto-mechanical experiments that has been applied successfully in several projects and studies. SimOptDevice can model a large number of optical elements and sensors which can be combined flexibly to cover a wide range of experimental setups.
We have explained the mathematical concepts within the library. A detailed description of our ray tracing and ray aiming procedures and of the determination of Jacobian matrices, needed for efficiently solving the nonlinear inverse problems, was given. This will be useful for readers interested in implementing virtual optical experiments. We also conclude that SimOptDevice can be used to simulate very complex opto-mechanical systems.
No data sets were used in this article.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Sensors and Measurement Systems 2018”. It is a result of the “Sensoren und Messsysteme 2018, 19. ITG-/GMA-Fachtagung”, Nürnberg, Germany, from 26 June 2018 to 27 June 2018.
The authors sincerely thank the EMPIR organization. The EMPIR is jointly funded
by the EMPIR participating countries within EURAMET and the European Union
(15SIB01: FreeFORM).
Edited by: Eric Starke
Reviewed by: two anonymous referees
Baer, G., Schindler, J., Pruss, C., Siepmann, J., and Osten, W.: Calibration of a non-null test interferometer for the measurement of aspheres and free-form surfaces, Opt. Express, 22, 31200, https://doi.org/10.1364/OE.22.031200, 2014. a
Bouillet, S. and Morin, C.: Method for the absolute measurement of the flatness of the surfaces of optical elements, Google Patents, US Patent App. 14/236,487, 2014. a
Cox, D., Little, J., and O'Shea, D.: Ideals, Varieties, and Algorithms: An Introduction to Computational and Commutative Algebra, 3rd Edn., Springer, New York, 2007. a, b
Dierl, M., Eckhard, T., Frei, B., Klammer, M., Eichstädt, S., and Elster, C.: Novel accuracy test for multispectral imaging systems based on ΔE measurements, J. Eur. Opt. Soc.-Rapid Publ., 14, 1, https://doi.org/10.1186/s41476-017-0069-1, 2018. a
Donato, L. D. and Crocco, L.: Model-Based Quantitative Cross-Borehole GPR Imaging via Virtual Experiments, IEEE T. Geosci. Remote, 53, 4178–4185, https://doi.org/10.1109/TGRS.2015.2392558, 2015. a
Ehret, G., Schulz, M., Stavridis, M., and Elster, C.: Deflectometric systems for absolute flatness measurements at PTB, Meas. Sci. Technol., 23, 094007, https://doi.org/10.1088/0957-0233/23/9/094007, 2012. a
Fortmeier, I.: Zur Optimierung von Auswerteverfahren für Tilted-Wave Interferometer, PhD thesis, University of Stuttgart, Stuttgart, ISBN: 978-3-923560-81-8, 2016. a
Fortmeier, I., Stavridis, M., Wiegmann, A., Schulz, M., Osten, W., and Elster, C.: Analytical Jacobian and its application to tilted-wave interferometry, Opt. Express, 22, 21313, https://doi.org/10.1364/OE.22.021313, 2014. a, b
Fortmeier, I., Stavridis, M., Wiegmann, A., Schulz, M., Osten, W., and Elster, C.: Evaluation of absolute form measurements using a tilted-wave interferometer, Opt. Express, 24, 3393, https://doi.org/10.1364/OE.24.003393, 2016. a
Fortmeier, I., Stavridis, M., Elster, C., and Schulz, M.: Steps towards traceability for an asphere interferometer, in: Optical Measurement Systems for Industrial Inspection X, Proc. SPIE, 10329, 1032939-1–1032939-9, https://doi.org/10.1117/12.2269122, 2017. a
Garbusi, E., Pruss, C., and Osten, W.: Interferometer for precise and flexible asphere testing, Opt. Lett., 33, 2973, https://doi.org/10.1364/OL.33.002973, 2008. a, b
Hao, Q., Wang, S., Hu, Y., Cheng, H., Chen, M., and Li, T.: Virtual interferometer calibration method of a non-null interferometer for freeform surface measurement, Appl. Optics, 55, 9992–10001, https://doi.org/10.1364/AO.55.009992, 2016. a
Hartley, R. and Zisserman, A.: Multiple View Geometry in computer vision, Cambridge University Press, Cambridge, 2003. a
Heißelmann, D., Franke, M., Rost, K., Wendt, K., Kistner, T., and Schwehn, C.: Determination of measurement uncertainty by simulation, arXiv:1707.01091 [physics], available at: http://arxiv.org/abs/1707.01091 (last access: February 2019), 2017. a
Hiller, J. and Reindl, L. M.: A computer simulation platform for the estimation of measurement uncertainties in dimensional X-ray computed tomography, Measurement, 45, 2166–2182, https://doi.org/10.1016/j.measurement.2012.05.030, 2012. a
Knudsen, E. B., Prodi, A., Baltser, J., Thomsen, M., Willendrup, P. K., d. Rio, M. S., Ferrero, C., Farhi, E., Haldrup, K., Vickery, A., Feidenhans'l, R., Mortensen, K., Nielsen, M. M., Poulsen, H. F., Schmidt, S., and Lefmann, K.: McXtrace: a Monte Carlo software package for simulating X-ray optics, beamlines and experiments, J. Appl. Crystallogr., 46, 679–696, https://doi.org/10.1107/S0021889813007991, 2013. a
Lieutenant, K., Zsigmond, G., Manoshin, S., Fromme, M., Bordallo, H. N., Champion, D., Peters, J., and Mezei, F.: Neutron instrument simulation and optimization using the software package VITESS, in: Proc. SPIE, 5536, 5536–5536-12, https://doi.org/10.1117/12.562814, 2004. a
MATLAB: release R2018b, The Mathworks, Inc., Natwick, MA, 2018. a
Schulz, M., Ehret, G., Stavridis, M., and Elster, C.: Concept, design and capability analysis of the new Deflectometric Flatness Reference at PTB, Nucl. Instrum. Meth. Phys. Res. Sect. A, 616, 134–139, https://doi.org/10.1016/j.nima.2009.10.108, 2010. a, b
Shen, H., Zhu, R., and Li, J.: Assessment of optical freeform surface error in tilted-wave-interferometer by combining computer-generated wave method and retrace errors elimination algorithm, Opt. Eng., 54, 074105, https://doi.org/10.1117/1.OE.54.7.074105, 2015. a
Soori, M., Arezoo, B., and Habibi, M.: Dimensional and geometrical errors of three-axis CNC milling machines in a virtual machining system, Computer-Aided Design, 45, 1306–1313, https://doi.org/10.1016/j.cad.2013.06.002, 2013. a
Trenk, M., Franke, M., and Schwenke, H.: The “Virtual CMM” a software tool for uncertainty evaluation – practical application in an accredited calibration lab, in: Proc. of ASPE: Uncertainty Analysis in Measurement and Design, American Society for Presicion Engineering, Rayleigh, NC, USA, 2004. a
Wiegmann, A., Stavridis, M., Walzel, M., Siewert, F., Zeschke, T., Schulz, M., and Elster, C.: Accuracy evaluation for sub-aperture interferometry measurements of a synchrotron mirror using virtual experiments, Precision Eng., 35, 183–190, https://doi.org/10.1016/j.precisioneng.2010.08.007, 2011. a, b





