the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Task-specific uncertainty estimation for medical CT measurements
Judith Bredemann
Robert H. Schmitt
Computed tomography (CT) is an important imaging technology for medical diagnosis purposes. However, by improving the CT scanners with regard to scan resolution and times, the use of CT is no longer limited to the diagnostic field. Different minimally invasive procedures are image-guided. CT-based surgical navigation utilizes 3-D measurements. Therefore, uncertainties in the imaging and image processing lead to erroneous initial conditions for the navigation process and result in a higher risk of unintended injuries of anatomical risk structures. To minimize the risk of unintended injuries, the uncertainties of the imaging process need to be estimated and considered during the planning of minimally invasive surgery. The estimation of uncertainties for medical measurements is still at the beginning though. Within this contribution, we show that it is important to consider the uncertainty of different measurement tasks during surgical planning using the example of minimally invasive surgery to the lateral skull base. A method for the task-specific uncertainty estimation is used to estimate the uncertainties for defined measurement tasks. Afterwards, we will discuss how the results have to be considered during the surgical planning process.
- Article
(3075 KB) - Full-text XML
- BibTeX
- EndNote
Over the past four decades, computed tomography (CT) has become the most important imaging technology in medicine. With a mean of 118.1 per 1000 population performed exams, it is widely used in the EU member states (OECD, 2016). But within the last few years, there has been a change in the application of CT data. Traditionally, CT data have especially been applied for the purpose of preventive medicine and diagnosis. In this context, the physician in charge performs a purely visual evaluation of the CT data. The aim could be for example the detection of a tumor or a fracture. Therefore, the image quality is the most important quality criterion for the assessment of the CT data. This means the images of the anatomical structures should have a high contrast and low noise. However, by improving the CT scanners with regard to scan resolution and times, the use of CT is no longer limited to the diagnostic field.
In order to perform surgical procedures more precisely, such as the delivery of implants, many surgeries are image-guided procedures. This means that the surgeon uses a surgical navigation system to track surgical instruments based on pre- or intraoperative images of the patient's anatomy. During an image-guided surgery, three-dimensional image data of the patient's anatomy and the patient's position are linked in the operating room. Surgical navigation systems are used to guide the surgical tools and project them onto the preoperative data in near-real time (Grosse et al., 2009).
CT and magnetic resonance imaging (MRI) systems are used to generate the required image data. Generated image data are used for 3-D coordinate measurements as they are the basis for guided movements of a surgical tool based on planned coordinates in 3-D space. The concrete measurement task consists of dimensionally stable imaging of anatomical structures in terms of their absolute dimensions and position in a fixed coordinate system (Pollmanns, 2014). Like all measurement processes, the imaging processes of CT and MRI are also subject to measurement uncertainties so that the position and the shape of the displayed anatomical structures differ from the real conditions.
Therefore, it is important to estimate the measurement uncertainty of these modalities in order to provide a sufficient safety distance between the guided surgical tool and risk structures to avoid unintended mechanical injuries (Bredemann et al., 2016). However, the definition and the concept of the measurement uncertainty is widely unknown in the medical field.
In the field of production engineering the determination of measurement uncertainties is an approved principle that is used to assess the capability of inspection processes. The evaluation of uncertainty is performed in accordance with the “Guide to the Expression of Uncertainty in Measurement” (GUM) (JCGM 100, 2008) and its supplements (JCGM 101, 2008; JCGM 102, 2011) by international agreement. All developed standards and procedures for the estimation of uncertainty are in compliance with the principles and wording defined in the GUM (Hernla et al., 2010). For the determination of the measurement uncertainty of coordinate measurements, there exist three different main approaches:
-
formulation of an analytical measurement uncertainty budget
-
simulation-based uncertainty determination
-
experimental procedures by means of a calibrated workpiece.
Since the measurement uncertainty of CT measurements is strongly influenced by the workpiece, analytic and simulation-based approaches are affected by significant limitations. According to VDI/VDE 2630 1-2 (2015) there are more than 60 factors that may influence the measurement result. These factors need to be considered during the mathematical modeling of the measurement process. An approach that can be used for estimating the uncertainty of CT measurement based on GUM recommendations has been presented by Dewulf et al. (2013). The uncertainty estimation concentrates on two major uncertainty contributors: voxel size and number of voxels. Weckenmann and Krämer (2010) as well as Wenig and Kasperl (2006) introduced early attempts to use simulations of the tomographic imaging process to estimate its uncertainty by generating uncertainty-induced noise on single-point measurements on a feature of interest. The results of the experimental validation are promising. However, the established models do not represent some influencing factors like the properties of the measured object properly and thus are incomplete so far.
Due to the limitations of the analytic and simulation-based approaches the experimental approach has been regarded as the most promising for determining the uncertainty of dimensional CT measurements so far (Bartscher et al., 2008; Kruth et al., 2011; VDI/VDE 2630 2-1, 2015; Carmignato et al., 2017). The experimental uncertainty determination was carried out by different studies for various measurement tasks (Bartscher et al., 2007; Bartscher et al., 2008; Carmignato and Savio, 2011; Schmitt et al., 2011). DIN EN ISO 15530-3 (2018) describes the procedure for the uncertainty determination based on calibrated workpieces for coordinate-measuring machines (CMMs). CT-specific standards are defined in VDI/VDE 2630 2-1 (2015). The method employs a calibrated reference object similar to the actual measured workpieces. Repeated measurements of defined measurement tasks are performed under comparable conditions to estimate the uncertainty of the regarding measurement process.
The evaluation and routine test of medical CT scanners is performed in accordance with DIN EN 61223-3-5 (2005). The standard defines the following performance indicators:
-
CT dose index (mGy)
-
mean CT number (HU)
-
pixel noise (HU)
-
homogeneity (HU)
-
spatial resolution (lp cm−1).
The mentioned indicators were developed to examine image quality and radiation exposure, but none of them analyzes whether the displayed anatomical structures are accurate to size. In addition, there are approaches that evaluate the image quality using anthropomorphic phantoms (Rau et al., 2013; Loubele et al., 2008) or geometric test specimens (e.g. cubes; Eggers et al., 2008). The studies are based on repeated measurements of diameters and distances and are similar to the procedure of experimental measurement uncertainty determinations. However, not all relevant uncertainty components are considered (Pollmanns, 2014). In addition, the results of the studies are only partially comparable due to the use of different test specimens. Therefore Pollmanns (2014) introduced a method for the task-specific measurement uncertainty estimation for medical CT measurements that is based on industrial standards. The core component of the method is a calibrated test specimen which can be used for the experimental uncertainty estimation for medical CT measurements. The test specimen allows the determination of systematic and random uncertainty components and therefore allows traceable measurements of anatomical structures for the first time. Pollmanns (2014) validated the experimental method by performing the uncertainty estimation for one specific measurement task (diameter of the upper semicircular canal) resulting from minimally invasive surgery to the lateral skull base. The uncertainty for just one specific measurement task is not sufficient for the planning of this highly complex surgery; the measurement uncertainties for further measurement tasks need to be known. In the following, the measurement uncertainty determination is expanded to further measurement tasks. Therefore the C-based planning of minimally invasive procedures to the lateral skull base is described as an example for image-guided surgery. Based on the described scenario additional measurement tasks are derived and the corresponding measurement uncertainties are estimated. Afterwards, it is discussed how the uncertainties for the different measurement tasks need to be considered during the planning phase of minimally invasive surgery to the lateral skull base. Subsequently, the determined uncertainty values are returned to the planning scenario by determining necessary minimal distances. Based on the results, further work for the patient individual risk assessment of minimally invasive surgery to the lateral skull base is discussed.
Procedures at the lateral skull base like the insertion of cochlear implants or the treatment of neuromata are very complex due to the anatomic complexity of the petrous bone and its neighboring structures. Risk structures such as the facial nerve and the jugular vein are embedded in bone, only a few millimeters apart. Therefore, surgeries are still performed under a wide exposure which implies a high risk of infection and longer recovery times (Stenin et al., 2014). Currently, methods for minimally invasive surgery of the lateral skull base are being developed to reduce the access trauma and to overcome the mentioned disadvantages. Especially the close neighborhood of risk structures is challenging and results in high requirements concerning submillimetric process deviations, high outcome predictability and reproducibility (Schipper et al., 2004).
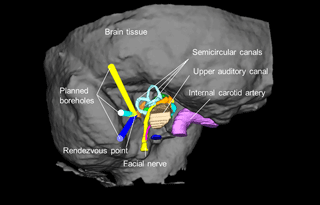
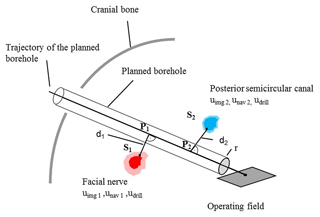
All concepts of minimally invasive surgery of the lateral skull base that have been attempted by different research groups are based on at least one tiny canal (called single-port, diameters 1–2 mm) that is drilled precisely to a defined target point (Labadie et al., 2014; Bell et al., 2013; Majdani et al., 2009). In the following sections, the concept of multiport image-guided minimally invasive surgery at the lateral skull base (MUKNO) is described in more detail. The method is based on three multiangular, linear ports (Fig. 1) that meet in a rendezvous point (Stenin et al., 2014).
2.1 Surgical planning
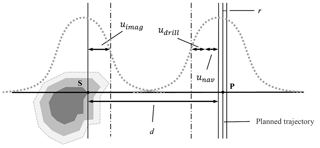
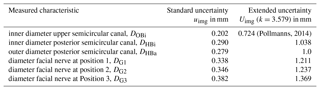
All ports need to be planned carefully in preoperative CT data of the patient's anatomy. Therefore, a high-resolution CT scan is performed and all critical anatomical structures are segmented manually. Afterwards, the planning of the boreholes is performed in the 3-D model of the patient's petrous bone. The surgeon defines the start and target point of the trajectory as well as the drill diameter of the boreholes in the medical planning software. Afterwards, all possible collision-free boreholes are calculated and visualized automatically. Only those boreholes are displayed that have a permissible distance to the risk structures. The minimal distance d depends on the process errors (random and systematic; Bredemann et al., 2016) and is defined as the perpendicular distance between the planned drill trajectory and the closest surface point of a risk structure. The drill does not hit a risk structure as long as the combined error ed is smaller than the minimal distance. According to Bredemann et al. (2016) ed is normally distributed with mean bd and variance (Eq. 1):
whereas ed is the sum of the following normally distributed error components (see Fig. 2):
-
the initial navigation error enav
-
the imaging error eimg
-
and the drilling process error edrill.
Nau-Hermes (2014) and Pollmanns (2014) proved already that the navigation error and the imaging error are approximately normally distributed. Based on the data of Kobler et al. (2014) it is assumed that the drilling error is normally distributed, too. Accordingly, bd and are calculated as follows (Eqs. 2 and 3) under the assumption that all errors are independent:
As the last step of the surgical planning, the surgeon manually selects three boreholes that are the best for the individual surgical intervention from his/her point of view. Afterwards, the regarding start and end points of the boreholes are transferred into the setting parameters of a custom-made navigation platform. The platform gives the initial pose of the surgical drill and enables the guidance of the drill.
2.2 Definition of measurement tasks
In order to emphasize the importance of dimensional measurements in the described planning of minimally invasive surgery to the lateral skull base, one possible planning scenario is discussed in the following (Fig. 3). Two boreholes are planned through the upper (cyan canal) and the posterior (yellow canal) semicircular canal. Furthermore, the yellow canal lies very close to the facial nerve.
The minimal distances between the surface of the risk structures and the planned boreholes are of high importance during the planning phase. Therefore, from a metrological point of view, the task of the imaging is to visualize the position and the contour of the different risk structures as accurately as possible.
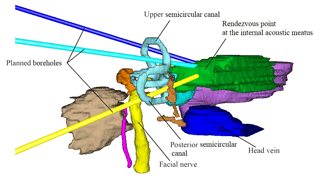
Figure 3Three planned boreholes. The planned target point is the internal auditory canal (based on Pollmanns, 2014).
Thus, the important inspection characteristic is the surface point that defines the minimal distance between the different risk structures and the planned boreholes. For each point along the boreholes the respective minimal distance to a risk structure is to be considered. Therefore, the point deviations of the following measurement tasks are important for the discussed planning scenario:
-
the inner diameter of the upper semicircular canal (Fig. 4)
-
the inner diameter of the posterior semicircular canal (Fig. 4)
-
the diameter on the outer surface of the posterior semicircular canal (Fig. 4)
-
the diameter of the facial nerve at different positions.
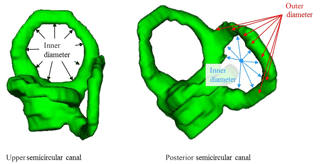
Figure 4Explanation of the “inner/outer” diameter for the upper and the posterior semicircular canal.
Since the imaging process and the following segmentation are affected by uncertainties, there are deviations in the measurement of the distances between the risk structures and the planned boreholes. Depending on the choice of gray level limit for the determination of the surface of the risk structures, the visualized surface points show a larger or smaller distance from the planned boreholes in comparison to the real anatomical structures. In addition, there are measurement deviations which result from a positional deviation of the entire anatomical structure related to a fixed origin. In the event that the set voxel size is significantly larger from the actual size of the risk structures, the total volume is subject to a scaling error.
Since the feasibility of the surgery depends primarily on whether the selected safety distance is large enough to compensate all uncertainties along the surgical process, the uncertainties along the surgical process need to be estimated. For the imaging process, it is important to consider random as well as systematical uncertainties because not all systematical influences can be eliminated. Furthermore, the uncertainties of the imaging and image processing need to be known for different measurement tasks. Depending on the surgical scenario different risk structures need to be considered when choosing the three boreholes with the largest safety distance.
The concept of measurement uncertainty is mostly unknown in the medical field. One approach that is based on the uncertainty estimation according to the industrial standard ISO 15530-3 (2018) has been attempted by Pollmanns (2014). ISO 15530-3 describes an experimental procedure for the uncertainty estimation of coordinate-measuring machine measurements that is based on measurements being made in the same way as the actual measurements, but with calibrated workpieces of similar dimensions and shape instead of the unknown workpieces to be measured. In the following, the general experimental procedure for task-specific uncertainty estimation of medical measurement tasks is described, and the uncertainties of the measurement tasks that were introduced in Sect. 2 are estimated.
3.1 Method
The core component of the measurement uncertainty estimation according to ISO 15530-3 is a calibrated workpiece. This workpiece has to be equal in dimensions, shape and material compared to future measuring objects. The normative requirements “geometrical similarity” and “similarity of material” are to be understood in the medical context as “anatomical similarity” and “radiometric similarity”.
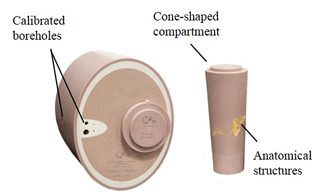
Therefore, Pollmanns (2014) developed a special medical test specimen that meets the normative requirements. Shape and size of the test specimen are based on the anatomical properties of the human skull and are constructed in layers from different CT-equivalent materials. Pollmanns used materials that represent soft tissue, skin tissue, cancellous bone, cortical bone as well as brain tissue. An insert which represents an artificial petrous bone is also part of the test specimen. In this insert, there are drill holes of different diameters, which imitate the ventilated areas of the petrous bone and are accessible from the outside for calibration purposes (Fig. 5). Systematical deviations can be determined by repeated measurements of the calibrated drill holes. The calibration of the holes of different diameter was performed in the form of repeat measurements on a CMM. In addition to the artificial petrous bone, there is also an interchangeable, cone-shaped compartment with an integrated human petrous bone so that the uncertainty from the measurement process up can be estimated by means of real anatomical structures. The necessary referencing of the individual CT datasets can be performed with the help of five ruby balls admitted on the front side of the test specimen (Pollmanns, 2014).
ISO 15530-3 prescribes that at least 20 repeat measurements have to be carried out to estimate a task-specific uncertainty. During the measurements, the position and orientation of the test specimen have to be varied to consider possible process variations of the position of the patient's head. Therefore the specimen is repositioned after every single scan. A custom-made fixture that is used for the positioning of the test specimen allows the variation in a limited space that is comparable to possible variations of the patient's head in the regarding fixture of the CT scanner (Pollmanns, 2014). The following uncertainty budget is defined by the standard (15530-3), to calculate the measurement uncertainty of the imaging and image processing (Eq. 4):
The standard uncertainty of the calibration of the drill holes ucal can be taken from the calibration certificate. However, the standard uncertainties from the measurement process up and the standard uncertainty resulting from systematic deviations ub are calculated from the repeat measurements. The standard uncertainty arising from variations of the workpiece material uw is to be understood as the anatomical differences between the different patients. For the estimation of uw further repeat measurements are necessary. Therefore, the uncertainty contribution uw was initially approximated as 2∕3 standard uncertainty of the measurement process (Pollmanns, 2014) by a group of experienced physicians and metrologists.
3.2 Results
In order to determine the measurement uncertainties of the described measurement tasks (see Sect. 3), a total of 21 repeat measurements were carried out on a medical cone beam CT at the University Hospital in Düsseldorf. The scan parameters correspond to a defined standard protocol, which is used for computer-tomographical scans of real petrous bones (see Table 1).
The test specimen was placed on the patient table using a rigid foam plate and a special foam fixture. After each measurement, the position of the test specimen was changed within the expected process variations. Two experienced physicians of the ENT Department of the University Hospital of Düsseldorf segmented the risk structures, the calibrated drill holes and the ruby balls for the uncertainty estimation. In order to determine the measurement uncertainties, the segmented datasets were imported into a commercial voxel processing software to determine the surface points and calculate the corresponding point deviations of the relevant diameter values.
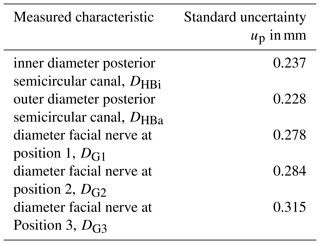
The procedure described in the following is repeated for every single measurement task. One dataset is selected randomly as the reference. In this reference set, measurement points are defined according to the respective measurement task. In order to be able to detect both position and shape deviations, the datasets to be evaluated are aligned using a defined coordinate system (based on the ruby balls) and are overlaid with the reference dataset. As a result, the point shifts between the measurements points are given and their standard uncertainties are calculated. The standard uncertainty of the measurement process up is the maximal calculated standard uncertainty for the regarding measurement task (Table 2). The uncertainty of the inner diameter of the upper semicircular canal was estimated by Pollmanns to up=0.162 mm.
The uncertainty of the measurement process is the smallest for the measurement of the internal diameter of the upper semicircular canal with 0.162 mm. In contrast, the uncertainty for the determination of the diameter of the facial nerve at position three is greater by a factor of 1.94. The measurement of the facial nerve at position three is subject to the greatest uncertainty, and the results for the measurement of the internal or external diameter of the posterior semicircular canals deviate by 0.009 mm from each other.
With ucal=0.005 mm, mm and up (Pollmanns, 2014) uimg is calculated (see Table 3).
The results of the uncertainty estimation for different measurement tasks mean that different uncertainties of the imaging and image processing need to be considered when the minimal distances di are calculated during the planning. In the following, the general procedure is performed for the yellow borehole (Fig. 2) that lies close to the facial nerve and passes through the posterior semicircular canal (Fig. 6).
For the determination of the critical distances d1 and d2 we assume that all systematic errors are compensated or fully covered in the uncertainty budget for the calculation of the regarding variance (bd=0) in the first approximation. Strategies for the compensation of systematic errors of the initial drill positioning were presented by Nau-Hermes (2014). The uncertainty of the drilling process udrill remains constant and is set to udrill=0.049 mm according to Kobler et al. (2014). The uncertainty of the navigation process unav varies depending on the drilled distance and can be calculated as follows:
where uβ is the uncertainty of the navigation process at the maximal drill distance (80 mm) for minimally surgery of the lateral skull base and li the drilled distance. According to Nau-Hermes (2014), uβ is set to 0.317 mm. For the following example, the point P1 is assumed to be in the middle of the planned trajectory of the borehole and P2 is assumed to be at 3∕4 of the planned trajectory. This leads to unav 1=0.159 mm and unav 2=0.23775. We assume that all deviations from the planned path that occur at point P1 or P2 lie in the interval defined by ed (Eq. 1) with a probability of 99.73 %. For the calculation of d1 and d2, the largest standard uncertainty estimated for the facial nerve is used to estimate the safe side. Under the above-mentioned assumptions, it can be stated that the planned canals are only valid if d1 > 1.160 mm and d2 > 1.052 mm. Studies of the distance from the planned drill trajectory to the nearest risk structure for the planning scenario show that the available space lies in the range of 1.3–3 mm for 10 patients (Nau-Hermes, 2014). Since the critical distances are defined between the drill and the regarding risk structure, the drill diameter needs to be considered. Currently, drill diameters of 1.5–2 mm are used for minimally invasive surgery to the lateral skull base (Bredemann et al., 2017), so that a distance of 0.55–2.25 mm remains maximal. The calculated minimal distances are feasible for 4 out of 10 patients. For the other patients, there is not enough distance between the drill and the risk structures so that they could not benefit from minimally invasive surgery to the lateral skull base. In order to estimate the safe side, in practice, a safety distance would be calculated from the minimal distance by multiplication by a safety factor. Therefore the innovative approach of minimally invasive surgery to the lateral skull base is limited to few patients at the moment.
The results for the uncertainty estimation of the measurement process up depend on the specific measurement task. Due to the lack of comparative values it is not reasonable to discuss the magnitude of the estimated uncertainties at this point. However, it remains to be noted that the determination of the diameter of the facial nerve at various positions is afflicted with the greatest uncertainties. Since the diameter of the facial nerve is significantly smaller in comparison to the inner and outer diameter of the semicircular canals, a greater influence of the segmentation on the result is expected.
The influence of standard uncertainty from the measuring process up is the relevant uncertainty contribution to uimg. This influence is amplified by estimating the uncertainty of the material uw based on up. The extended uncertainties Uimg are 2 to 3.5 times the voxel size and thus lie in the expected range for CT measurements. During the segmentation, it was found that there are differences between the CT images of the test specimen and real human skulls. The images of the test specimen appear to be noisier. Furthermore, the grayscale limit is defined between bone and air and not between bone and soft tissue like in CT images of the human skull. Therefore a detailed examination of the differences between the test specimen and the natural example is necessary. The measurement tasks considered in this contribution are all derived from one planning scenario. Accordingly, further scenarios need to be discussed to extend the uncertainty analysis of the imaging and image processing. In addition, we expect an influence of the individual patient on the uncertainty of the imaging and image processing, similar to the influence of the specific workpiece on industrial CT measurements. To analyze this influence further investigations involving different compartments for the test specimen are planned. In general, the database for the uncertainty estimation of medical CT measurements by means of the test specimen is limited. Due to ethical considerations, the number of compartments with integrated anatomical structures is restricted. Therefore the combination of the stated approached with simulation-based approaches seems to be promising to expand the uncertainty estimation to a larger group of patients. This approach will be the subject of further research efforts.
The calculated critical distances d1 and d2 depend on the uncertainties along the surgical process and on the confidence level that is chosen for the calculation of ed. In a first step, a confidence level of 99.73 % was chosen based on industrial standards (ISO 22514-1, 2016) for the capability assessment. Whether this confidence level is sufficient in a medical context needs to be discussed in an interdisciplinary team, and the confidence level for further investigations has to be defined. It remains to be noted that the approach of minimally invasive surgery is still limited to few patients. To implement the procedures in width, it would be necessary to optimize the surgical process so that the uncertainties of the whole process can be reduced. In addition, it is desirable to further anchor the uncertainty concept for risk assessment of surgical processes. Thereby the results of different research groups could be compared in a more easy and reasonable manner.
Computed tomography is an important medical image modality. CT-based surgical navigation utilizes 3-D measurements. Uncertainties in the imaging and image processing lead to erroneous start conditions for the navigation process. The uncertainties of the imaging and image processing together with the uncertainties of the other process steps result in the risk of unintended injuries of anatomical risk structures. Therefore, the uncertainty of imaging and image processing needs to be considered during surgical planning. Using the example of minimally invasive surgery to the lateral skull base, different measurement tasks were derived from a specific planning scenario. Using a special test specimen the task-specific uncertainties for the imaging and image processing were estimated and transferred into the planning by calculating the critical distances between the planned boreholes and the facial nerve and the posterior semicircular canal.
Different analyses are needed to estimate the uncertainty of the imaging and image process more precisely. It has to be analyzed whether the usage of the test specimen instead of a human skull for the uncertainty estimation has an influence. Repeat measurements with different compartments need to be performed to consider the influence of different patients on the uncertainty estimation. Furthermore, other measurement tasks will be derived from other planning scenarios.
The datasets generated during and analyzed during the current study are not publicly available but are available from the corresponding author on request.
The general procedure and the test specimen for the uncertainty estimation were developed by Pollmanns. Pollmanns estimated the uncertainty for the inner diameter of the upper semicircular canal as well. The authors of this contribution derived further measurement tasks from the surgical planning scenario and transferred the results of the uncertainty estimation back into the surgical planning to calculate feasible safety distances for the first time.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Evaluating measurement data and uncertainty”. It is not associated with a conference.
We would like to thank the German Research Foundation (DFG) for the support and the funding
of the depicted research. Moreover we would like to thank our project partners from university hospital
Düsseldorf:
Jörg Schipper, Julia Kristin and Igor Stenin.
This is an updated and revised version of a paper written in German language and published in “Technisches Messen 84 (2017) 2” in 2017.
It is published in JSSS with the kind permission of the publisher De Gruyter.
Edited by: Klaus-Dieter Sommer
Reviewed by: two anonymous referees
Bartscher, M., Hilpert, U., Goebbels, J., and Weidemann, G.: Enhancement and Proof of Accuracy of Industrial Computed Tomography (CT) Measurements, CIRP Annals, 56, 495–498, https://doi.org/10.1016/j.cirp.2007.05.118, 2007.
Bartscher, M., Hilpert, U., and Fiedler, D.: Determination of the measurement uncertainty of computed tomography measurements using a cylinder head as an example, Tech. Mess., 75, 178–186, 2008.
Bell, B., Gerber, N., Williamson, T., Gavaghan, K., Wimmer, W., Caversaccio, M., and Weber, S.: In vitro accuracy evaluation of image-guided robot system for direct cochlear access, in: Otology & neurotology: official publication of the American Otological Society, American Neurotology Society and European Academy of Otology and Neurotology, 34, 1284–1290, https://doi.org/10.1097/MAO.0b013e31829561b6, 2013.
Bredemann, J., Voigtmann, C., Schmitt, R., Stenin, I., Kristin, J., Klenzner, T., and Schipper, J.: Determining the patient's risk in minimally invasive surgery to the lateral skull base, in: 15. CURAC Annual Conference – Tagungsband der Jahrestagung der Deutschen Gesellschaft für computer- und roboterassistierte Chirurgie e.V., 29 September–1 October 2016, Bern/Swiss, 155–161, 2016.
Bredemann, J., Voigtmann, C., Jantzen, M., and Schmitt, R. H.: Bohrkopfintegrierte Sensorik zur Absicherung medizinischer Bohrprozesse, Tagungsband der 16. Jahrestagung der Deutschen Gesellschaft für Computer- und Roboterassisstierte Chirurgie, Hannover, 2017.
Carmignato, S. and Savio, E.: Traceable volume measurements using coordinate measuring systems, CIRP Annals, 60, 519–522, https://doi.org/10.1016/j.cirp.2011.03.061, 2011.
Carmignato, S., Dewulf, W., and Leach, R.: Industrial X-ray Computed Tomography, Springer Publisher, ISBN: 978-3-319-59571-9, 2017.
Dewulf, W., Kiekens, K., Tan, F., Welkenhuyzen, and Kruth, J.-P.: Uncertainty determination and quantification for dimensional measurements with industrial computed tomography, CIRP Annals, 62, 535–538, https://doi.org/10.1016/j.cirp.2013.03.017, 2013.
DIN EN 61223-3-5: Bewertung und routinemäßige Prüfung in Abteilungen für medizinische Bildgebung – Teil 3-5: Abnahmeprüfungen: Leistungsmerkmale zur Bildgebung von Röntgeneinrichtungen für Computertomographie (IEC 61223-3-5:2004), 2005.
Eggers, G., Klein, J., Welzel, T., and Mühling, J.: Geometric accuracy of digital volume tomography and conventional computed tomography, Brit. J. Oral Max. Surg., 46, 639–644, 2008.
Grosse, J., von Walter, M., and Jakse, G.: Endoskopie, minimal invasive chirurgische und navigierte Verfahren in der Urologie, edited by: Wintermantel, E. and Ha, S. W., Medizintechnik, Springer, Berlin, Heidelberg, 2009.
Hernla, M., Wendt, K., and Franke, M.: Aufgabenspezifische Messunsicherheit von Koordinatenmessungen, Tech. Mess., 77, 607–615, https://doi.org/10.1524/teme.2010.0067, 2010.
ISO 15530-3: Geometrical product specifications (GPS) – Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement – Part 3: Use of calibrated workpieces or measurement standards, 2018.
ISO 22514-1: Statistical methods in process management – Capability and performance – Part 1: General principles and concepts (ISO 22514-1:2014), 2016.
JCGM 100: Evaluation of measurement data – Guide to the expression of uncertainty in measurement, Joint Committee for Guides in Metrology, 2008.
JCGM 101: Evaluation of Measurement Data – Supplement 1 to the Guide to the Expression of Uncertainty in Measurement – Propagation of Distributions Using a Monte Carlo Method, Joint Committee for Guides in Metrology, 2008.
JCGM 102: Evaluation of Measurement Data – Supplement 2 to the Guide to the Expression of Uncertainty in Measurement – Extension to Any Number of Output Quantities, Joint Committee for Guides in Metrology, 2011.
Kobler, J., Schoppe, M., Lexow, G. J., Rau, T. S., Majdani, O., Kahrs, L. A., and Ortmaier, T.: Temporal bone borehole accuracy for cochlear implantation influenced by drilling strategy: an in vitro study, Int. J. Comput. Ass. Rad., 9, 1033–1043, https://doi.org/10.1007/s11548-014-0997-9, 2014.
Kruth, J. P., Bartscher, M., Carmignato S., Schmitt R., de Chiffre, L., and Weckenmann, A.: Computed tomography for dimensional metrology, CIRP Annals, 60, 821–842, https://doi.org/10.1016/j.cirp.2011.05.006, 2011.
Labadie, R., Balachandran, R., Noble, Jack H., Blachon, G., Mitchell, J., and Reda, F. A.: Minimally invasive image-guided cochlear implantation surgery: first report of clinical implementation, Laryngoscope, 124, 1915–1922, https://doi.org/10.1002/lary.24520, 2014.
Loubele, M., van Assche, N., Carpentier, K., Maes, F., Jacobs, R., van Steenberghe, D., and Suetens, P. : Comparative localized linear accuracy of small-field cone-beam CT and multislice CT for alveolar bone measurements, Oral Surg. Oral Med. O., 105, 512–518, 2008.
Majdani, O., Rau, T. S., Baron, S., Eilers, H., Baier, C., and Heimann, B.: A robot-guided minimally invasive approach for cochlear implant surgery: preliminary results of a temporal bone study, Int. J. Comput. Ass. Rad., 4, 475–486, https://doi.org/10.1007/s11548-009-0360-8, 2009.
Nau-Hermes, M.: Ein messtechnischer Beurteilungsansatz für das Verletzungsrisiko anatomischer Strukturen bei bildgestützten minimalinvasiven Eingriffen, Aachen, Hochschulbibliothek der Rheinisch-Westfälischen Technischen Hochschule Aachen, 2014
OECD/EU: Health at a Glance: Europe 2016 – State of Health in the EU Cycle, OECD Publishing, Paris, https://doi.org/10.1787/9789264265592-en, 2016
Pollmanns, S.: Bestimmung von Unsicherheitsbeiträgen bei medizinischen Computertomografiemessungen für die bildbasierte navigierte Chirurgie, 1. Aufl, Aachen, Apprimus Verlag, Fertigungstechnik & Qualitätsmanagement, Bd. 2014, 29, 2014.
Rau, T. S., Würfel, W., Lenarz, T., and Majdani, O.: Three-dimensional histological specimen preparation for accurate imaging and spatial reconstruction of the middle and inner ear, Int. J. Comput. Ass. Rad., 8, 481–509, https://doi.org/10.1007/s11548-013-0825-7, 2013.
Schipper, J.,Klenzner, T., Aschendorff, A., Arapakis, I., Ridder, G. J., and Laszig, R.: Navigiert-kontrollierte Kochleostomie – Ist eine Verbesserung der Ergebnisqualität in der Kochleaimplantat-Chirurgie möglich?, HNO, 52, 329–335, https://doi.org/10.1007/s00106-004-1057-5, 2004.
Schmitt, R., Damm, B., and Niggemann, C.: Messunsicherheitsbestimmung für die industrielle Computertomografie anhand kalibrierter Bauteile, Tech. Mess., 78, 133–141, 2011.
Stenin, I., Hansen, S., Becker, M., Sakas, G., Fellner, D., Klenzner, T., and Schipper, J.: Minimally invasive multiport surgery of the lateral skull base, BioMed research international 2014, p. 379295, https://doi.org/10.1155/2014/379295, 2014.
VDI/VDE 2630 Part 2.1: 2015-06 – Computed tomography in dimensional measurement – Determination of the uncertainty of measurement and the test process suitability of coordinate measurement systems with CT sensors, VDI, Düsseldorf, 2015.
Weckenmann, A. and Krämer, P.: Computed Tomography for Application in Manufacturing Metrology, Key Engineering Materials, 437, 73–78, https://doi.org/10.4028/www.scientific.net/KEM. 437.73, 2010.
Wenig, P. and Kasperl, S.: Examination of the measurement uncertainty on dimensional measurements by x-ray computed tomography, Proceedings of 9th European Conference on Non-Destructive Testing, Berlin, Germany, 2006.
- Abstract
- Introduction
- Minimally invasive surgery to the lateral skull base
- Estimating the uncertainty of different measurement tasks
- Transfer of results into surgical planning
- Discussion
- Conclusions and outlook
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Abstract
- Introduction
- Minimally invasive surgery to the lateral skull base
- Estimating the uncertainty of different measurement tasks
- Transfer of results into surgical planning
- Discussion
- Conclusions and outlook
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- References