the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Combined resistive and thermoelectric oxygen sensor with almost temperature-independent characteristics
Murat Bektas
Thomas Stöcker
Angelika Mergner
Gunter Hagen
Ralf Moos
The present study is focused in two directions. In the first part, BaFeAl0.01TaxO3−δ (BFATx) thick films with a Ta content between 0.1 and 0.4 were manufactured using the novel room temperature coating method “aerosol deposition” (ADM), and its material properties were characterized to find the best composition of BFATx for temperature-independent oxygen sensors. The material properties “Seebeck coefficient” and “conductivity” were determined between 600 and 800 ∘C at different oxygen partial pressures. BaFe0.69Al0.01Ta0.3O3−δ (BFAT30) was found out to be very promising due to the almost temperature-independent behavior of both the conductivity and the Seebeck coefficient. In the second part of this study, films of BFAT30 were prepared on a special transducer that includes a heater, equipotential layers, and special electrode structures so that a combined direct thermoelectric/resistive oxygen sensor of BFAT30 with almost temperature-independent characteristics of both measurands, Seebeck coefficient and conductance could be realized. At high oxygen partial pressures (pO2 > 10−5 bar), the electrical conductance of the sensor shows an oxygen sensitivity of m = 0.24 (with m being the slope in the logσ vs. logpO2 representation according to the behavior of σαpO), while the Seebeck coefficient changes with a slope of −38 µV K−1 per decade of pO2 at 700 ∘C. However, at low pO2 (pO2 < 10−14 bar) the conductance and the Seebeck coefficient change with pO2, with a slope of m = −0.23 and −21.2 µV K−1 per decade pO2, respectively.
In order to minimize environmental pollution and to increase air quality, combustion processes, e.g., in internal combustion engines or gas burners, have to be controlled. Since there is a relationship between the equilibrium oxygen partial pressure in the exhaust or flue gas and the air-to-fuel ratio, combustion processes can be monitored by measuring the oxygen concentration (Riegel, 2002). Potentiometric solid-state electrolyte oxygen sensors, e.g., applied as so-called lambda probes in harsh automotive exhaust environments, show a very good stability but they need a stable reference atmosphere (Guth and Zosel, 2004). Amperometric oxygen sensors, which do not need reference gas, are not cost-effective due to their more complex design (Ivers-Tiffée et al., 2001). Another alternative to the above-mentioned potentiometric and amperometric oxygen sensors at high temperatures and in harsh environments are resistive-type sensors with their relatively inexpensive simple design (Moos et al., 2011). Film-type resistive oxygen gas sensors based on semiconducting metal oxides like SnO2 (Sakai et al., 2001), TiO2 (Logothetis and Kaiser, 1983), SrTiO3 (Gerblinger et al., 1995), Ga2O3 (Fleischer and Meixner, 1991), or other materials have been intensively investigated. The resistivity of the gas sensing films Rsensor changes with the analyte concentration of the ambience. In the case of oxygen as the analyte, the oxygen partial pressure, pO2, is of relevance (Eq. 1):
In Eq. (1), EA is the activation energy for conduction, kB the Boltzmann constant, and T the temperature. The exponent m is a measure for the oxygen sensitivity of the sensor or the sensor material. As can be seen from Eq. (1), the resistance of the sensor material does not respond only to the oxygen concentration of the atmosphere but it also changes with temperature. Only a limited number of semiconducting oxides have been found that show a low or even negligible temperature dependency of the resistance, such as La2CuO4 (Blase et al., 1997), LaFe0.8Cu0.2O3 (Sahner et al., 2006), La0.05Sr0.05Ti0.65Fe0.35O3−δ (LSTF) (Moos et al., 2003), SrTi0.65Fe0.35O3−δ (STF35) (Rothschild et al., 2005), and BaFe1−xTaxO3−δ (BFT) (Moseley and Williams, 1989). Since the most investigated sensor material STF35 is not stable towards sulfur oxide poisoning (Rettig et al., 2004) and decomposes under rich conditions, we recently focused on BFT (Bektas et al., 2014a, b) as a temperature-independent oxygen sensor to control combustion processes.
On the other hand, the measurand “sensor resistance” is not only dependent on the material property “resistivity” but also depends on the film geometry and on the film morphology (Rettig and Moos, 2007a). Abrasion, cracks, or particle sintering may affect the sensor resistance and, hence, may reduce long-term stability, which is a key issue for industrial application of resistive gas sensors.
In contrast to resistive gas sensors, in direct thermoelectric gas sensors (DTEGS), the Seebeck coefficient S is measured. The Seebeck coefficient S is a material property that depends on the analyte concentration. To obtain a thermoelectric voltage UGSF, a temperature difference ΔT has to be applied between two electrodes of the sensor film.
Since UGSF is a path-independent quantity, UGSF is less affected by cracks or abrasion and DTEGS offer a far better long-term stability than resistive devices of the same material (Rettig and Moos, 2007b).
DTEGS have already been successfully demonstrated for materials like SrTi0.6Fe0.4O3−δ (STF40), a material that is also known as a temperature-independent resistive oxygen sensor material (Rettig and Moos, 2007a), for SnO2 (Ionescu, 1998; Rettig and Moos, 2007b), or Li-doped NiO (Matsumiya et al., 2002) for hydrogen gas sensing. Rettig and Moos (Rettig and Moos, 2008) pointed out that most of the materials for resistive gas sensing are also good candidates for DTEGS, since the Seebeck coefficient and resistivity of a material change simultaneously with the concentration of mobile charge carriers. The latter are dependent on the analyte concentration. Especially for oxide materials, the Seebeck coefficient, which in literature is sometimes also referred to as thermopower, is an important parameter to determine charge carrier densities to determine constants for defect chemical models of these semiconductor materials; see e.g., Jonker (1968), Choi and Tuller (1988), and Rothschild et al. (2005).
In this study, we focus on BaFeAl0.01TaxO3−δ (abbreviated as BFATx). The study is focused in two directions. In the first part, BFATx thick films with a Ta content of x=0.1–0.4 were manufactured using the novel room temperature coating method “aerosol deposition” (ADM or AD method), and their material properties Seebeck coefficient and conductivity were determined between 600 and 800 ∘C at different oxygen partial pressures. The ADM allows dense ceramic coatings to be produced completely without any high-temperature processes directly from an initial bulk powder on almost any substrate material. Further details on the ADM are given for instance in the reviews of Akedo (2004, 2006) or Hanft et al. (2015).
In the second part of this study, films were prepared on a special transducer that includes a heater, equipotential layers, and special electrode structures so that a combined direct thermoelectric/resistive oxygen sensor of BFAT30 with almost temperature-independent characteristics of both measurands, S and R, could be realized.
BaFeAl0.01TaxO3−δ (BFATx) ceramic powders were synthesized in the mixed oxide technique, using commercially available BaCO3 (Alfa Aesar, 99 %), Fe2O3 (Alfa Aesar, 98 %), Al2O3 (Almatis, CL 3000, 99.8 %), and Ta2O5 (Alfa Aesar, 99 %) as starting materials. To obtain BFAT powders, the raw materials were calcined at 1350 ∘C in air for 15 h. Detailed information on the powder preparation can be found in an earlier publication (Bektas et al., 2014a).
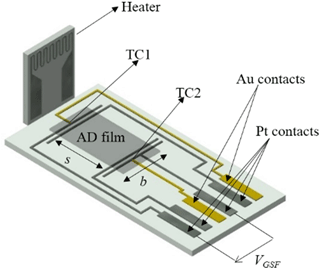
To determine the material properties Seebeck coefficient and conductivity of the ADM-processed films between 600 and 800 ∘C, a planar setup (in the following denoted as transducer) as depicted in Fig. 1 was used. The transducer exhibited four platinum electrodes and two gold-platinum thermocouples (TC1, TC2). Platinum (LPA 88-11S, Heraeus) and gold (DuPont 5744) pastes were screen-printed on alumina substrates (96 % Al2O3). The Pt and Au leads were sintered at 950 and at 850 ∘C in air, respectively. In order to avoid an interaction between the BFATx thick films and contact pastes (Pt and Au) during the sintering process, the leads had already been contacted with wires before the films were deposited by the aerosol deposition method. The contacted substrates were fired at 950 ∘C for 20 min. Finally, dense BFATx thick films were obtained by ADM. A similar setup to simultaneously determine the electrical conductivity and the Seebeck coefficient of films can be found by Stöcker et al. (2016). To form the aerosol and to transport the aerosol, nitrogen with a flow rate of 4 L min−1 served as carrier gas. A slit nozzle with an orifice size of 10 × 0.5 mm2 was used. The shaking frequency of the vibration table was adjusted 400 min−1 and the distance between the nozzle and substrate was kept at 4 mm. With the X–Y stage, the substrate was moved at a velocity of 1 mm s−1. By adjusting the process time, AD films with thicknesses between 3 and 5 µm were produced. After the coating process, the samples were heat-treated at 850 ∘C for 3 h in air, which is just 50 ∘C higher than the maximum test temperature.
In order to determine the four-probe DC resistance of the films between the Pt contacts (current applied to outer contacts; voltage taken between the inner contacts with the distance s; see Fig. 1), a Keithley 2700 digital multimeter was used in the offset-compensated resistance measurement mode. The electrical conductivity σ (or the resistivity ρ) was derived from the measured resistance and the geometrical parameters (see Fig. 1) according to Eq. (3).
Here, s is the spacing between the Pt electrodes, R the measured resistance, and A the cross-section area of the sample (b⋅t), with the film thickness t, and the sample width b.
To measure the thermovoltage UGSF, an alternating temperature gradient over the specimens was generated using a separate heater that was placed some millimeters apart (see Fig. 1). A sinusoidal signal with a frequency of 10 mHz was applied to the heater and the thermovoltage UGSF(t) and the temperature difference ΔT(t) between the two Pt contacts (determined by the two thermocouples TC1 and TC2) were recorded. From the slope in the UGSF vs. ΔT plot, the Seebeck coefficient of the material vs. Pt can be derived.
It has to be corrected by the Seebeck coefficient of platinum, SPt, at the sensor temperature (Eq. 4). For a more detailed description of the data evaluation, refer to Rettig and Moos (2009). A similar procedure is described in Sect. 3.2 for the sensor device.
In order to heat the gas sensitive film to operation temperature, the setup according to Fig. 1 was placed in a small tube furnace. Oxygen partial pressures pO2 in the range of 10−5 to 1 bar were varied using N2 / O2 gas mixtures. For low pO2 values, water-saturated N2 / H2 (5 % H2 in N2) gas mixtures were used. An yttrium-stabilized ZrO2 lambda probe was used to control the actual pO2 close to the sensor. Detailed information about the calculation of pO2 from the lambda-probe data can be found in Moos and Härdtl (1997).
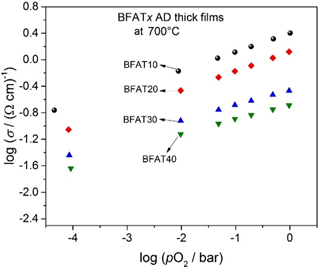
Figure 2Double logarithmic representation of the electrical conductivity (σ) vs. the oxygen partial pressure (pO2) of BFATx AD thick films at 700 ∘C.
3.1 Conductivity and Seebeck coefficient of BFATx
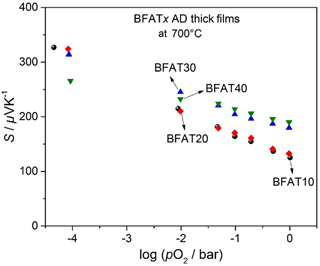
In a double logarithmic representation, Fig. 2 shows the electrical conductivity σ against the oxygen partial pressure pO2 of BFATx AD thick films at 700 ∘C in the non-reducing range. Since the increasing tantalum content reduces the number of oxygen vacancies (Bektas et al., 2014b), the electrical conductivity decreases. The electrical conductivity of samples increases with increasing pO2 as expected for a p-type semiconducting oxide. The results are in good agreement with BFATx bulk materials (Bektas et al., 2014b).
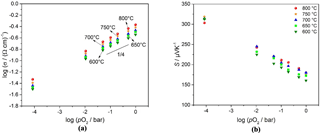
Figure 4(a) Double logarithmic representation of electrical conductivity vs. pO2 and (b) a semilogarithmic representation of the Seebeck coefficient vs. pO2 of BFAT30 AD thick film between 600 and 800 ∘C.
The relation between electron concentration n as well as defect electron concentration p (holes) and electrical conductivity for n- and p-type semiconductors are given by Eq. (5a) and (5b). Here, e denotes the electron charge, μn the mobility of electrons, and μp the mobility of holes.
and
Similarly, the relation between n or p and the Seebeck coefficients Sn and Sp are given by Eq. (6a) and (6b) for a classical, nondegenerate semiconductor (Choi and Tuller, 1988),
and
where k is the Boltzmann constant, NC is the effective density of states in the conduction band, NV is the effective density of states in the valence band, and the respective transport parameters are denoted by Ae and Ah.
A semilogarithmic representation of the Seebeck coefficient and pO2 of BFATx thick films at 700 ∘C is shown in Fig. 3. The samples have a positive Seebeck coefficient that decreases with increasing pO2, a behavior that is again typical for p-type electrical semiconductors. Figures 2 and 3 also reveal that both the electrical conductivity and the Seebeck coefficient of samples are pO2-dependent.
AD thick films with a composition of x = 0.3 (BFAT30) show a very interesting additional behavior. Not only the double logarithmic representation of the electrical conductivity vs. pO2 is almost temperature-independent between 700 and 800 ∘C, as is revealed by Fig. 4a. The electrical conductivity of the sensor material shows almost a O2 dependence and increases with increasing temperature with a slight activation energy of 0.16 eV as can be derived from the slope of an Arrhenius-like representation (lgσ vs. 1∕T) at constant pO2 (1 bar). Also the Seebeck coefficient of the BFAT30 AD thick film is almost independent of temperature between 700 and 800 ∘C but is strongly dependent on pO2 as Fig. 4b shows.
These results demonstrate that a combined temperature-independent oxygen sensor with both thermoelectric and resistivity independency may be obtained when using BFAT30 as the sensor material. The development of such a sensor will be reported on in the next section.
3.2 Combined thermoelectric–resistive oxygen sensor device
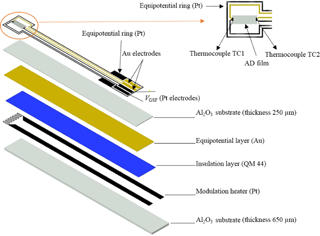
The experimental setup to determine the Seebeck coefficient of the films has been depicted in Fig. 1. In this setup, the modulation heater and the measurement part including the sensor film and electrodes are separated. Although this setup is useful for materials' characterization, it is not appropriate for sensor application. Therefore, a similar sensor setup to that used in Rettig and Moos (2009) was used. The combined thermoelectric–resistive oxygen sensor is sketched in Fig. 5. While the modulation heater was screen-printed on 96 % Al2O3 substrate with dimensions 56 × 6.35 × 0.65 mm3, gold and platinum leads were screen-printed on a separate 96 % Al2O3 substrate (50.08 × 6.35 × 0.25 mm3). An equipotential layer (Au) was coated onto the reverse side of this substrate. The equipotential layer has been used to avoid crosstalk between the modulation voltage and the measured thermovoltage as explained in Rettig and Moos (2007a). After preparation of these two separate substrates, they were bonded together using a commercially available insulation ink, dried, and fired. In contrast to the previously investigated DTEGS (Rettig and Moos, 2007a, b), the gas sensitive film was formed using the ADM at room temperature. Moos et al. (2003) showed that during high-temperature firing, elements diffuse between the sensor layer and the alumina substrate. Therefore an additional diffusion barrier layer had to be applied when using a classical printing and firing technique. Sahner et al. (2009) investigated AD-prepared STF and pointed out that – since ADM is a room temperature coating method – there is no more need for such a diffusion barrier anymore.
Figure 6 shows the applied sinusoidal voltage of the modulation heater U (bottom), the thermovoltage of the gas sensitive film UGSF, which is the sensor raw signal, and the temperature difference ΔT, all as a function of time. The modulation heater was modulated with a periodic voltage . Then, a temperature difference on the sensor forms with a frequency fmod:
Since there is a quadratic relation between the heater power P and the applied modulation heater voltage (, the temperature difference ΔT changes with the double frequency ( (Rettig and Moos, 2007a). Since 10 mHz modulation frequency was applied, ΔT varied with a frequency of 20 mHz. It is obvious from Fig. 6 that there is no crosstalk between the sensor layer and the modulation heater.
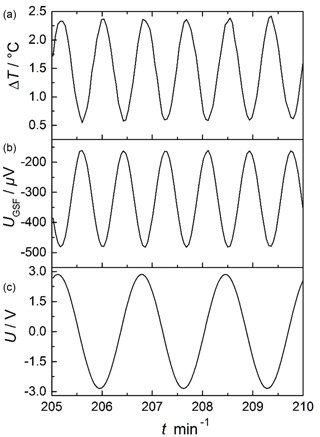
Figure 6Example of a typical measurement, here for 650 ∘C in O2: raw signal of the applied sinusoidal voltage by the function generator U (c), thermovoltage of the gas sensitive film UGSF (b), and temperature difference ΔT (a).
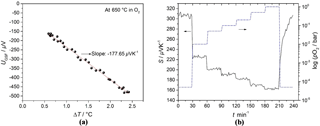
Figure 7(a) Example of a regression analysis in an oxygen atmosphere and (b) the pO2 dependence of the Seebeck coefficient of BFAT30 AD thick film at 650 ∘C.
If one takes one data point of UGSF and ΔT each second and plots them against each other, one obtains a straight line. This is shown in Fig. 7a for the recorded data of Fig. 6 (example for sensor operation temperature of 650 ∘C in O2). Through a regression analysis, the slope can be determined. Applying Eq. (4) yields the Seebeck coefficient S. The thermovoltage of the gas sensitive film varies with changing temperature difference. This procedure was repeated 18 times with a period of 100 s for 30 min before a new oxygen partial pressure step was set at the same temperature. The maximal error of the Seebeck coefficient calculated from regression analysis is ±3.5 µV K−1 in N2 and ±1.3 µV K−1 in 1 bar O2. The relative error in pO2 is below ±1 %. Figure 7b shows the pO2 dependence of the Seebeck coefficient of the BFAT30 AD thick film at 650 ∘C. Since the Seebeck coefficient is positive, in the high pO2 range (pO–1 bar), a p-type conduction mechanism is prevalent. As can be seen, the sensor follows the stepwise changing pO2 within a little less than 1 min (t90=51 s). If one considers the volume of the sensor chamber including piping and the gas flow velocity, one obtains a typical time constant of 15 s, which is in the same order as the response time. So, it is assumed that the sensor response time is limited by the gas exchange of the gas supply and may be probably intrinsically even faster.
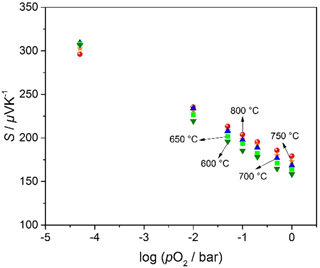
Figure 8 shows the Seebeck coefficient as it depends on pO2 and on the sensor operation temperature between 600 and 800 ∘C. Assuming a constant transport factor Ah, and using Eqs. (5b) and (6b), the temperature dependence of the Seebeck coefficient for a nondegenerate p-type semiconductor (Eq. 8) can be written (Moos et al., 1995) as follows:
Thus, the Seebeck coefficient should increase by almost 298 µV K−1 per temperature decade for a typical p-type conductor. Moos et al. (1995) investigated the Seebeck coefficient of n-type Sr1−xLaxTiO3. They found an increase of the Seebeck coefficient of samples between x=0.01 and x=0.1 with a slope of −298 µV K−1 per temperature decade from room temperature to 900 ∘C.
As expected, S decreases with increasing pO2 but is – in contrast to the expected results for nondegenerate semiconductors – almost independent of temperature in the investigated temperature range. This independence of the Seebeck coefficient on temperature may be explained with a hopping-type transport model, the so-called small polaron hopping mechanism (Tuller and Nowick, 1977). Such a very low temperature dependence of the Seebeck coefficient has up to now not yet been found for other semiconducting materials for DTEGS.
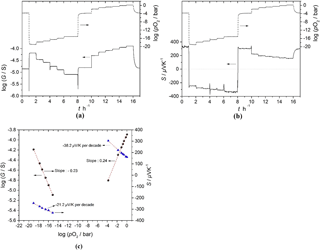
Figure 9(a) Oxygen partial pressure dependence of conductance and (b) the Seebeck coefficient of BFAT30 AD thick film, and (c) sensor characteristics obtained from panels (a) and (b) as a point graph at 700 ∘C in the pO2 range 10−21–1 bar.
Only if one uses oxide-ion-conducting YSZ (zirconium oxide with 8 mol % Y2O3), a negligible temperature dependence of the Seebeck coefficient has been observed. For ion-conducting DTEGS, however, this can be explained easily, since what is really measured is the entropy, which is (at least at first order) independent of the sensor temperature (Röder-Roith et al., 2009).
The sensor response was also determined in the pO2 range between 10−21 and 1 bar at 700 ∘C. In this case, the DC resistance of the sensor material was measured using the two-probe technique (Fig. 5). In addition, as can be seen from Fig. 5, only point-like contacts were used. Therefore, instead of the electrical conductivity, the electrical conductance G ( was used. The pO2 dependence of the electrical conductance, the Seebeck coefficient, and the obtained sensor characteristics are given in Fig. 9a, b, and c, respectively. Figure 9a and b show that the electrical conductance and the Seebeck coefficient of the ADM sensor film material change fast with a reproducible response to the changing pO2, both in reducing and in oxidizing atmospheres at 700 ∘C. Since the sensor material shows an n- to p-type transition when the atmosphere changes from reducing to oxidizing (or vice versa), the Seebeck coefficient changes its sign. At high pO2 (pO2 > 10−5 bar), the electrical conductance shows an oxygen sensitivity of dlgG ∕ dlgpO2=m ≈ 0.24 according to the behavior of σ∝pO, while the Seebeck coefficient changes with a slope of −38 µV K−1 per decade of pO2 at 700 ∘C. The theoretical expected value for nondegenerate p-type band-like semiconducting oxides with the slope m should be m × ln 10 × µV K−1 per decade pO2 (Choi et al., 1986; Rettig and Moos, 2007a). The reason for this difference may be attributed to the small polaron hopping mechanism in the valence band. By combining Eqs. (5b), (6b), and a pO2 dependence of the electrical conductivity of σ∝pO, for a p-type semiconductor the relationship between the pO2 and the Seebeck coefficient can be obtained. It can be easily seen that the pre-conditions for the derivation of −49 µV K−1 per decade pO2 are that both the effective density of states in the valence band (NV) and the mobility μp of the defect electrons do not depend on pO2. This is definitely not the case if small polaron hopping prevails.
At low pO2 (pO2 < 10−14 bar), the electrical conductance and the Seebeck coefficient change with pO2 with a slope of and −21.2 µV K−1 per decade pO2, respectively. When considering the entire pO2 range, it is clear that typical oxide materials that may be applied as temperature-independent p-type resistive sensors cannot be operated without ambiguity since below the pO2 of the intrinsic conductivity minimum, the sensor becomes n-type conductive and the conductivity increases again with decreasing pO2. As shown in Fig. 9b, the Seebeck coefficient also does not depend monotonically on pO2. In fact, it shows an S-like behavior, with the steepest slope around the intrinsic conductivity minimum (Jonker, 1968). However, when combining both responses, i.e., the conductivity and the Seebeck coefficient, one may derive an unambiguous response, with the highest sensitivity in the medium pO2 range. This is exactly the range in which modern gasoline engines have to be operated to achieve a high catalyst efficiency (Ivers-Tiffée et al., 2001) because around stoichiometric conditions (λ=1; λ is the air-fuel-ratio), the pO2 varies around 14 to 16 decades (Riegel, 2002). The oxygen sensor should have a high response to pO2 at this point. Although it is more complicated to determine the Seebeck coefficient than to measure just the resistance, the high sensitivity around λ=1 is of great advantage.
It has to be noted here that it is not a new idea to use the Seebeck coefficient as the measurand. Basically, all metal oxides with oxygen equilibration kinetics that are fast enough can be applied. However, when using films of BFAT30, one gets the additional advantage that, in oxidizing atmospheres, the characteristics of both the conductivity and the Seebeck coefficient depend on pO2 and both are almost temperature-independent.
The first part of this study dealt with the electrical material properties of aerosol-deposited BFATx thick films. The Seebeck coefficient S and the electrical conductivity σ were investigated between 600 and 800 ∘C for different oxygen partial pressures between 10−5 and 1 bar. BFAT30 was found to be a candidate material for a combined thermoelectric–resistive oxygen sensor due to its very low temperature dependence of both the electrical conductivity and the Seebeck coefficient. In the second part, combined thermoelectric–resistive oxygen sensors from BFAT30 with a special transducer and modulation heater were fabricated and tested. As expected from the material characterization data, the Seebeck coefficient of the sensor material is strongly dependent on the partial pressure of oxygen, but is almost temperature-independent. The material can be operated even in very reducing atmospheres, with a low response time.
A temperature modulation frequency of 10 mHz, which has been chosen for this initial study, results in a period of 100 s. Since such a response time is too high for many practical applications (Rettig and Moos, 2007a), the temperature modulation frequency has to be increased. Applying a method that is suggested in the literature (Rettig and Moos, 2009) is expected to reduce the measurement time by 2 or 3 decades.
All relevant data presented in the article are stored according to institutional requirements and as such are not available online. However, all data used in this manuscript can be made available upon request to the authors.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Sensor/IRS2 2017”. It is a result of the AMA Conferences, Nuremberg, Germany, 30 May–1 June 2017.
The authors would like to thank the German Research Foundation (DFG) for funding
under grant MO1060/22-1.
Edited by: Peter A. Lieberzeit
Reviewed by: two anonymous referees
Akedo, J.: Aerosol Deposition Method for Fabrication of Nano Crystal Ceramic Layer, Mater. Sci. Forum, 449–452, 43–48, https://doi.org/10.4028/www.scientific.net/MSF.449-452.43, 2004.
Akedo, J.: Aerosol Deposition of Ceramic Thick Films at Room Temperature: Densification Mechanism of Ceramic Layers, J. Am. Ceram. Soc., 89, 1834–1839, https://doi.org/10.1111/j.1551-2916.2006.01030.x, 2006.
Bektas, M., Hanft, D., Schönauer-Kamin, D., Stöcker, T., Hagen, G., and Moos, R.: Aerosol-deposited BaFe0.7Ta0.3O3−δ for nitrogen monoxide and temperature-independent oxygen sensing, J. Sens. Sens. Syst., 3, 223–229, https://doi.org/10.5194/jsss-3-223-2014, 2014a.
Bektas, M., Schönauer-Kamin, D., Hagen, G., Mergner, A., Bojer, C., Lippert, S., Milius, W., Breu, J., and Moos, R.: BaFe1−xTaxO3−δ – A material for temperature independent resistive oxygen sensors, Sensor. Actuat. B-Chem., 190, 208–213, https://doi.org/10.1016/j.snb.2013.07.106, 2014b.
Blase, R., Härdtl, K. H., and Schönauer, U.: Oxygen Sensor Based on Non-Doped Cuprate, U.S. Patent 5,792,666, 1997.
Choi, G. M. and Tuller, H. L.: Defect Structure and Electrical Properties of Single-Crystal Ba0.03Sr0.97TiO3, J. Am. Ceram. Soc., 71, 201–205, https://doi.org/10.1111/j.1151-2916.1988.tb05848.x, 1988.
Choi, G. M., Tuller, H. L., and Goldschmidt, D.: Electronic-transport behavior in single-crystalline Ba0.03Sr0.97TiO3, Phys. Rev. B, 34, 6972–6979, https://doi.org/10.1111/j.1151-2916.1988.tb05848.x, 1986.
Fleischer, M. and Meixner, H.: Gallium oxide thin films: a new material for high-temperature oxygen sensor, Sensor. Actuat. B-Chem., 4, 437–441, https://doi.org/10.1016/0925-4005(91)80148-D, 1991.
Gerblinger, J., Hausner, M., and Meixner, H.: Electric and Kinetic Properties of Screen-Printed Strontium Titanate Films at High Temperatures, J. Am. Ceram. Soc., 78, 1451–1456, https://doi.org/10.1111/j.1151-2916.1995.tb08836.x, 1995.
Guth, U. and Zosel, J.: Electrochemical solid electrolyte gas sensors – hydrocarbon and NOx analysis in exhaust gases, Ionics, 10, 366–377, https://doi.org/10.1007/BF02377996, 2004.
Hanft, D., Exner, J., Schubert, M., Stöcker, T., Fuierer, P., and Moos, R.: An Overview of the Aerosol Deposition Method: Process Fundamentals and New Trends in Materials Applications, J. Ceram. Sci. Technol., 6, 147–182, https://doi.org/10.4416/JCST2015-00018, 2015.
Ionescu, I.: Combined Seebeck and resistive SnO2 device gas sensors, a new selective, Sensor. Actuat. B-Chem., 48, 392–394, https://doi.org/10.1016/S0925-4005(98)00077-X, 1998.
Ivers-Tiffée, E., Härdtl, K. H., Menesklou, W., and Riegel, J.: Principles of solid state oxygen sensors for lean combustion gas control, Electrochim. Acta, 47, 807–814, https://doi.org/10.1016/S0013-4686(01)00761-7, 2001.
Jonker, G. H.: The Application of combined conductivity and Seebeck-effect plots for the analysis of semiconductor properties, Philips Res. Rep., 23, 131–138, 1968.
Logothetis, E. M. and Kaiser, W. J.: TiO2 film oxygen sensors made by chemical vapour deposition from organometallics, Sensor. Actuat., 4, 333–340, https://doi.org/10.1016/0250-6874(83)85041-0, 1983.
Matsumiya, M., Qiu, F., Shin, W., Izu, N., Murayama, N., and Kanzaki, S.: Thin-film Li-doped NiO for thermoelectric hydrogen gas sensor, Thin Solid Films, 419, 213–217, https://doi.org/10.1016/S0040-6090(02)00762-9, 2002.
Moos, R. and Härdtl, K. H.: Defect Chemistry of Donor-Doped and Undoped Strontium Titanate Ceramics between 1000∘ and 1400 ∘C, J. Am. Ceram. Soc., 80, 2549–2562, https://doi.org/10.1111/j.1151-2916.1997.tb03157.x, 1997.
Moos, R., Gnudi, A., and Härdtl, K.H.: Thermopower of Sr1−xLaxTiO3 ceramics, J. Appl. Phys., 78, 5042–5047, https://doi.org/10.1063/1.359731, 1995.
Moos, R., Rettig, F., Hürland, A., and Plog, C.: Temperature-independent resistive oxygen exhaust gas sensor for lean-burn engines in thick-film technology, Sensor. Actuat. B-Chem., 93, 43–50, https://doi.org/10.1016/S0925-4005(03)00333-2, 2003.
Moos, R., Izu, N., Rettig, F., Reiß, S., Shin, W., and Matsubara, I.: Resistive Oxygen Gas Sensors for Harsh Environments, Sensors, 11, 3439–3465, https://doi.org/10.3390/s110403439, 2011.
Moseley, P. and Williams, D. E.: Gas sensors based on oxides of early transition metals, Polyhedron, 8, 1615–1618, 1989.
Rettig, F. and Moos, R.: Direct thermoelectric gas sensors: Design aspects and first gas sensors, Sensor. Actuat. B-Chem., 123, 413–419, https://doi.org/10.1016/j.snb.2006.09.002, 2007a.
Rettig, F. and Moos, R.: Direct Thermoelectric Hydrocarbon Gas Sensors Based on SnO2, IEEE Sens. J., 7, 1490–1496, https://doi.org/10.1109/JSEN.2007.906887, 2007b.
Rettig, F. and Moos, R.: Morphology dependence of thermopower and conductance in semiconducting oxides with space charge regions, Solid State Ionics, 179, 2299–2307, https://doi.org/10.1016/j.ssi.2008.08.006, 2008.
Rettig, F. and Moos, R.: Temperature-modulated direct thermoelectric gas sensors: thermal modeling and results for fast hydrocarbon sensors, Meas. Sci. Technol., 20, 65205, https://doi.org/10.1088/0957-0233/20/6/065205, 2009.
Rettig, F., Moos, R., and Plog, C.: Poisoning of temperature independent resistive oxygen sensors by sulfur dioxide, J. Electroceram., 13, 733–738, https://doi.org/10.1007/s10832-004-5184-x, 2004.
Riegel, J.: Exhaust gas sensors for automotive emission control, Solid State Ionics, 152–153, 783–800, https://doi.org/10.1016/S0167-2738(02)00329-6, 2002.
Röder-Roith, U., Rettig, F., Röder, T., Janek, J., Moos, R., and Sahner, K.: Thick-film solid electrolyte oxygen sensors using the direct ionic thermoelectric effect, Sensor. Actuat. B-Chem., 136, 530–535, https://doi.org/10.1016/j.snb.2008.12.024, 2009.
Rothschild, A., Litzelman, S. J., Tuller, H. L., Menesklou, W., Schneider, T., and Ivers-Tiffée, E.: Temperature-independent resistive oxygen sensors based on SrTi1−xFexO3−δ solid solutions, Sensor. Actuat. B-Chem., 108, 223–230, https://doi.org/10.1016/j.snb.2004.09.044, 2005.
Sahner, K., Straub, J., and Moos R.: Cuprate-ferrate compositions for temperature independent resistive oxygen sensors, J. Electroceram., 16, 179–186, https://doi.org/10.1007/s10832-006-6203-x, 2006.
Sahner, K., Kaspar, M., and Moos, R.: Assessment of the novel aerosol deposition method for room temperature preparation of metal oxide gas sensor films, Sensor. Actuat. B-Chem., 139, 394–399, https://doi.org/10.1016/j.snb.2009.03.011, 2009.
Sakai, G., Baik, N. S., Miura, N., and Yamazoe, N.: Gas sensing properties of tin oxide thin films fabricated from hydrothermally treated nanoparticles Dependence of CO and H2 response on film thickness, Sensor. Actuat. B-Chem., 77, 116–121, https://doi.org/10.1016/S0925-4005(01)00682-7, 2001.
Stöcker, T., Exner, J., Schubert, M., Streibl, M., and Moos, R.: Influence of Oxygen Partial Pressure during Processing on the Thermoelectric Properties of Aerosol-Deposited CuFeO2, Materials, 9, 227, https://doi.org/10.3390/ma9040227, 2016.
Tuller, H. L. and Nowick, A. S.: Small polaron electron transport in reduced CeO2 single crystals, J. Phys. Chem. Solids, 38, 859–867, https://doi.org/10.1016/0022-3697(77)90124-X, 1977.